
分析 (1)运用向量数量积的坐标表示和模的公式,结合二倍角的余弦公式化简f(x),再由余弦函数的图象可得增区间;
(2)求得g(x)的解析式,令t=cosx(0≤t≤1),即有g(t)=2t2-4λt-1=2(t-λ)2-1-2λ2,运用二次函数的最值的求法,讨论对称轴和区间的关系,即可得到所求值.
解答 解:(1)向量$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),向量$\overrightarrow{b}$=(cos$\frac{x}{2}$,-sin$\frac{x}{2}$).
可得$\overrightarrow{a}$•$\overrightarrow{b}$=cos$\frac{3}{2}$xcos$\frac{x}{2}$-sin$\frac{3}{2}$xsin$\frac{x}{2}$=cos($\frac{3x}{2}$+$\frac{x}{2}$)=cos2x,
|$\overrightarrow{a}$|=$\sqrt{co{s}^{2}\frac{3x}{2}+si{n}^{2}\frac{3x}{2}}$=1,|$\overrightarrow{b}$|=$\sqrt{co{s}^{2}\frac{x}{2}+si{n}^{2}\frac{x}{2}}$=1,
f(x)=|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{1+1+2cos2x}$=$\sqrt{2×2co{s}^{2}x}$=2|cosx|,
由y=|cosx|的图象可得f(x)的增区间为(kπ-$\frac{π}{2}$,kπ),k∈Z;
(2)g(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|=cos2x-4λ|cosx|=2cos2x-1-4λ|cosx|,
令t=cosx(0≤t≤1),即有g(t)=2t2-4λt-1=2(t-λ)2-1-2λ2,
当λ>1时,区间[0,1]为减区间,即有t=1时,取得最小值,
且为1-4λ=-$\frac{3}{2}$,解得λ=$\frac{5}{8}$<1,不成立;
当0<λ≤1时,区间[0,λ]为减区间,[λ,1]为增区间,
即有t=λ时,取得最小值,
且为-1-2λ2=-$\frac{3}{2}$,解得λ=$\frac{1}{2}$.
综上可得λ=$\frac{1}{2}$.
点评 本题考查向量的数量积的坐标表示和模的公式的运用,考查三角函数的化简和求值,注意运用换元法,化为二次函数的最值求法,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
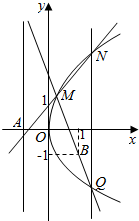 如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).
如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
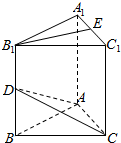 如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.
如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com