
设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足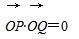
(1)求m的值;
(2)求直线PQ的方程.
[解析] (1)曲线方程为(x+1)2+(y-3)2=9表示圆心为(-1,3),半径为3的圆.
∵点P、Q在圆上且关于直线x+my+4=0对称,
∴圆心(-1,3)在直线上,代入得m=-1.
(2)∵直线PQ与直线y=x+4垂直,
∴设P(x1,y1)、Q(x2,y2),PQ方程y=-x+b
将直线y=-x+b代入圆方程,得
2x2+2(4-b)x+b2-6b+1=0
Δ=4(4-b)2-4×2×(b2-6b+1)>0,得
2-3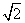 <b<2+3
<b<2+3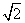 .
.
由韦达定理得
x1+x2=b-4①,x1x2=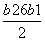 ②
②
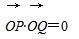 即2x1x2-b(x1+x2)+b2=0
即2x1x2-b(x1+x2)+b2=0
将①②代入得:b2-6b+1-b2+4b+b2=0
解得b=1,经验证知符合题意
∴PQ方程为y=-x+1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知方程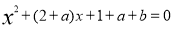 的两根是
的两根是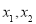 ,且
,且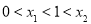 ,则
,则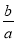 的取值范围是( )
的取值范围是( )
A、(-2,-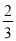 ) B、[-2,-
) B、[-2,-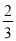 ) C、(-1,-
) C、(-1,-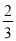 ) D、(-2,-1)
) D、(-2,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是( )
A.x+y-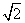 =0 B.x+y+1=0
=0 B.x+y+1=0
C.x+y-1=0 D.x+y+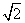 =0
=0
查看答案和解析>>
科目:高中数学 来源: 题型:
设A为圆(x+1)2+y2=4上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为( )
A.(x+1)2+y2=25 B.(x+1)2+y2=5
C.x2+(y+1)2=25 D.(x-1)2+y2=5
查看答案和解析>>
科目:高中数学 来源: 题型:
从椭圆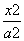 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
A.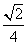 B.
B.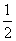
C.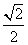 D.
D.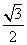
查看答案和解析>>
科目:高中数学 来源: 题型:
四棱锥P-ABCD中,AB、AD、AP两两垂直,AB=1,AD=2,AP=3,F为PC的中点,E为PD上,且PD=3PE,用
(1)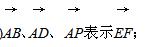
(2)求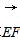 的模.
的模.
查看答案和解析>>
科目:高中数学 来源: 题型:
某校高三年级的学生共1000人,一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取50人了解情况,则80~90分数段应抽取________人.
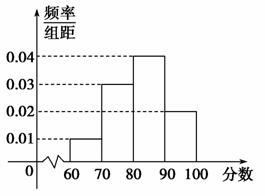
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com