
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx﹣2与椭圆C交于A,B两点,点P(0,1),且|PA|=|PB|,求直线l的方程.
【答案】解:(Ⅰ)由椭圆的定义可得2a=6,2c=2 ![]() , 解得a=3,c=
, 解得a=3,c= ![]() ,
,
所以b2=a2﹣c2=3,
所以椭圆C的方程为 ![]() +
+ ![]() =1.
=1.
(Ⅱ)由 ![]()
得(1+3k2)x2﹣12kx+3=0,
由于直线与椭圆有两个不同的交点,
所以△=144k2﹣12(1+3k2)>0解得 ![]() .
.
设A(x1 , y1),B(x2 , y2)
则 ![]() ,
, ![]() ,
,![]() ,
,
所以,A,B中点坐标E( ![]() ,
, ![]() ),
),
因为|PA|=|PB|,所以PE⊥AB,即kPEkAB=﹣1,
所以 ![]() k=﹣1
k=﹣1
解得k=±1,
经检验,符合题意,
所以直线l的方程为x﹣y﹣2=0或x+y+2=0
【解析】(Ⅰ)由椭圆的定义可得a,由焦距的概念可得c,再由a,b,c的关系可得b,进而得到椭圆方程;(Ⅱ)直线l:y=kx﹣2代入椭圆方程,运用韦达定理和判别式大于0,再由中点坐标公式和两直线垂直的条件,可得k的方程,解方程可得直线方程.


科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?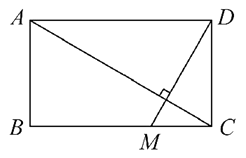
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,导函数f'(x)的图象如图所示,则函数f(x)( ) 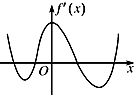
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数为t=﹣ ![]() ,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣
,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣ ![]() ρsinθ=8+2
ρsinθ=8+2 ![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com