
分析 利用复数的运算法则、共轭复数的意义、复数相等的定义即可得出.
解答 解:设z=a+bi(a,b∈R,b≠0),则$z+\frac{1}{z}=(a+\frac{a}{{{a^2}+{b^2}}})+(b-\frac{b}{{{a^2}+{b^2}}})i∈R$,
得:$b-\frac{b}{{{a^2}+{b^2}}}=0$,即a2+b2=1 ①
又由|z-2|=2,得(a-2)2+b2=4 ②
解①②组成的方程组得:$\left\{\begin{array}{l}a=\frac{1}{4}\\ b=±\frac{{\sqrt{15}}}{4}\end{array}\right.$
所以 $z=\frac{1}{4}±\frac{{\sqrt{15}}}{4}i$
点评 本题考查了复数的运算法则、共轭复数的意义、复数相等,考查了推理能力与计算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 980 | 410 | 60 |
| 女生 | 340 | 150 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a?α,b?α,c⊥a,c⊥b 则c⊥α | B. | 若a⊥α,b⊥α 则a∥b | ||
| C. | 若a∥α,α∩β=b 则a∥b | D. | 若b?α,a∥b 则 a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
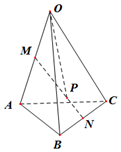 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -2 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com