
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,函数y=cos$({x-\frac{3π}{2}})$=cos($\frac{3π}{2}$-x)=-sinx是奇函数;
②,比如α=300、β=3900是第一象限角且α<β,则tanα=tanβ;
③,函数y=tanx的对称中心为($\frac{kπ}{2}$,0),由2×$(-\frac{3π}{8})$+$\frac{π}{4}$=-$\frac{π}{2}$,得y=tan$({2x+\frac{π}{4}})$的图象关于点$({-\frac{3π}{8},0})$对称;
④,函数y=2sin$({\frac{π}{4}-2x})$+1的单调递减区间是$[{kπ-\frac{π}{8},kπ+\frac{3π}{8}}]\;({k∈Z})$;
解答 解:对于①,函数y=cos$({x-\frac{3π}{2}})$=cos($\frac{3π}{2}$-x)=-sinx是奇函数,故①正确;
对于②,比如α=300、β=3900是第一象限角且α<β,则tanα=tanβ,故②错;
对于③,函数y=tanx的对称中心为($\frac{kπ}{2}$,0),由2×$(-\frac{3π}{8})$+$\frac{π}{4}$=-$\frac{π}{2}$,得y=tan$({2x+\frac{π}{4}})$的图象关于点$({-\frac{3π}{8},0})$对称,故③正确;
对于④,函数y=2sin$({\frac{π}{4}-2x})$+1的单调递减区间是$[{kπ-\frac{π}{8},kπ+\frac{3π}{8}}]\;({k∈Z})$.故④错;
故选:B
点评 本题考查了命题真假的判定,涉及到三角函数的知识,属于中档题.


科目:高中数学 来源: 题型:解答题
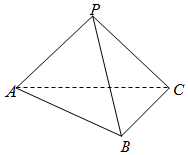 如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | [-1,2] | C. | $({\frac{1}{2},6})$ | D. | $({\frac{1}{2},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意m∈A,都有f(m+3)>0 | B. | 任意m∈A,都有f(m+3)<0 | ||
| C. | 存在m∈A,都有f(m+3)=0 | D. | 存在m∈A,都有f(m+3)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com