
分析 令t=2x2-3x+1,求出其单调性区间,则g(t)=($\frac{1}{2}$)t是单调递减,根据复合函数的单调性可得增区间.
解答 解:函数$f(x)={(\frac{1}{2})^{2{x^2}-3x+1}}$,
令t=2x2-3x+1,
则函数f(x)转化为g(t)=($\frac{1}{2}$)t是单调递减,
函数t=2x2-3x+1,
开口向上,对称轴x=$\frac{3}{4}$,
其单调性区间,单调增区间为:[$\frac{3}{4}$,+∞)单调减区间为(-∞,$\frac{3}{4}$];
根据复合函数的单调性“同增异减”可得函数f(x)的单调增区间为(-∞,$\frac{3}{4}$];
故答案为:$(-∞,\frac{3}{4}]$.
点评 本题考查了复合函数的单调性的求法.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
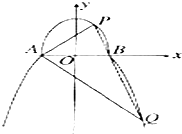 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com