
分析 本题考查了函数定义的求法.要使得函数f(x)有意义,则(x-1)•$\sqrt{{x}^{2}-x-2}$≥0 且 x2-x-2≥0.需要注意的是,需对x2-x-2=0和 x2-x-2>0 分类求解,再进行求并运算.
解答 解:要使得函数解析式$f(x)=\sqrt{(x-1)\sqrt{{x}^{2}-x-2}}$有意义
则(x-1)•$\sqrt{{x}^{2}-x-2}$≥0 且 x2-x-2≥0
当x2-x-2=0时,x=-1 或 2,能使得函数解析式有意义;
当 x2-x-2>0 时,可转换为$\left\{\begin{array}{l}{x-1≥0}\\{{x}^{2}-x-2>0}\end{array}\right.$⇒x>2
综上:f(x)的定义为:{-1}∪{x|x≥2}
所以本题答案为:{-1}∪{x|x≥2}
点评 本题考查了函数定义的求法,属于中档题.考生在答题时,需要注意求解过程的细节,函数定义域是高考常考题型.


科目:高中数学 来源: 题型:填空题
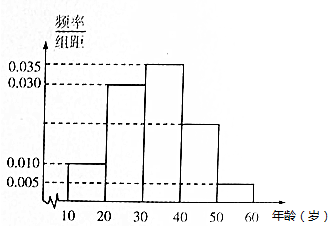 为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.
为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在x=1处取到极大值 | B. | f(x)在x=1处取到极小值 | ||
| C. | f(x)在x=0处取到极大值 | D. | f(x)在x=0处取到极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
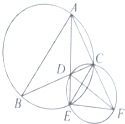 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com