
分析 数列{an}满足a${\;}_{n+1}^{2}$=anan+2(an≠0),可得:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n+2}}{{a}_{n+1}}$=q≠0,可得:数列{an}是等比数列.由0<a1<a6=1=${a}_{1}{q}^{5}$,可得q≠±1.a1a11=a2a10=…=a5a7=${a}_{6}^{2}$=1,n≥12时,an=${a}_{6}{q}^{n-6}$≠1.因此a1-$\frac{1}{{a}_{1}}$+${a}_{11}-\frac{1}{{a}_{11}}$=a1-$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{1}}$-a1=0=…,即可得出.
解答 解:∵数列{an}满足a${\;}_{n+1}^{2}$=anan+2(an≠0),
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n+2}}{{a}_{n+1}}$=q≠0,
∴数列{an}是等比数列.
∵0<a1<a6=1=${a}_{1}{q}^{5}$,∴q≠±1.
∴a1a11=a2a10=…=a5a7=${a}_{6}^{2}$=1,
n≥12时,an=${a}_{6}{q}^{n-6}$≠1.
∴a1-$\frac{1}{{a}_{1}}$+${a}_{11}-\frac{1}{{a}_{11}}$=a1-$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{1}}$-a1=0,
…,
则使不等式a1-$\frac{1}{{a}_{1}}$+a2-$\frac{1}{{a}_{2}}$+…+an-$\frac{1}{{a}_{n}}$≤0恒成立的n的最大值是11.
故答案为:11.
点评 本题考查了等比数列的通项公式及其性质、不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
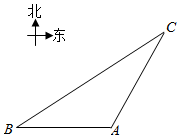 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | -12 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
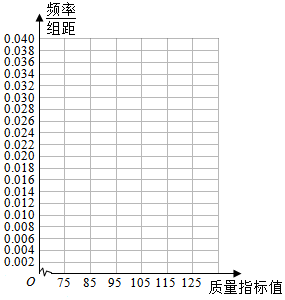
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
| 频数 | 6 | 26 | x | 22 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com