
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 画出图形,结合图形,利用平面向量加减运算的几何意义进行解答即可
解答 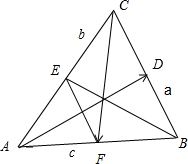 解:如图所示,
解:如图所示,
对于①,$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{CB}$=$-\frac{1}{2}\overrightarrow{BC}$,∴①错误;
对于②,$\overrightarrow{EA}=\overrightarrow{CE}=\overrightarrow{BE}-\overrightarrow{BC}$,∴②正确;
对于③,$\overrightarrow{AD}+\overrightarrow{BE}$=$\frac{1}{2}$($\overrightarrow{AC}+\overrightarrow{AB}$)+$\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BC}$)
=$\frac{1}{2}$($\overrightarrow{AC}+\overrightarrow{BC}$)=-$\overrightarrow{CF}$∴③正确;
所以正确的个数为2个;
故选C.
点评 本题考查了平面向量的加减及数乘运算的应用问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3413 | B. | 0.4772 | C. | 0.8185 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 7 | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
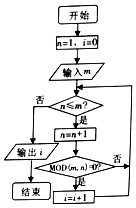 已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )
已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com