
分析 (Ⅰ)求导,利用导函数正负判断函数的单调性,进而得出函数的最值;
(Ⅱ)整理不等式得lnt-1+$\frac{1}{t}$≥0,只需求出式子lnt-1+$\frac{1}{t}$的最小值,利用导数求解即可;观察式子特点,构造式子令t=$\frac{n+1}{n}$ (t>1),利用上题结论代入计算.
解答 解:(Ⅰ)f(x)=xn-xn+1,
∴f'(x)=nxn-1-(n+1)xn
=-(n+1)xn-1(x-$\frac{n}{n+1}$);
令f'(x)=0,
得x=$\frac{n}{n+1}$,
当x∈(0,$\frac{n}{n+1}$),f'(x)>0,f(x)递增;
当x∈($\frac{n}{n+1}$,+∞),f'(x)<0,f(x)递减;
函数f(x)的最大值为f($\frac{n}{n+1}$)=$\frac{{n}^{n}}{{(n+1)}^{n+1}}$;
(Ⅱ)要证lnt≥1-$\frac{1}{t}$,
即证lnt-1+$\frac{1}{t}$≥0.
令h(t)=lnt-1+$\frac{1}{t}$,
h'(t)=$\frac{t-1}{{t}^{2}}$,
∴h(t)在(0,1)递减,(1,+∞)递增,
h(t)≥h(1)=0,
∴lnt≥1-$\frac{1}{t}$,
f(x)<$\frac{1}{ne}$的证明:
令t=$\frac{n+1}{n}$ (t>1)
∴ln$\frac{n+1}{n}$>$\frac{1}{n+1}$
∴(n+1)ln$\frac{n+1}{n}$>lne
∴$\frac{{(n+1)}^{n+1}}{{n}^{n+1}}$>e
∴$\frac{{n}^{n}}{{(n+1)}^{n+1}}$<$\frac{1}{ne}$
由(1)知f(x)<$\frac{{n}^{n}}{{(n+1)}^{n+1}}$<$\frac{1}{ne}$
点评 考查了导函数求最值的方法和构造式子,对试题进行探索式证明.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抛物线 | B. | 双曲线 | C. | 直线 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
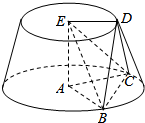 如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.
如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (3,+∞) | D. | (-∞,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com