
 如图,圆锥的高PO=$\sqrt{2}$,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则点B到平面PAC的距离( )
如图,圆锥的高PO=$\sqrt{2}$,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则点B到平面PAC的距离( )| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | 1 |
分析 由已知易得AC⊥OD,AC⊥PO,可证面POD⊥平面PAC,由平面垂直的性质考虑在平面POD中过O作OH⊥PD于H,则OH⊥平面PAC,在Rt△OHC中,求得OH,点B到平面PAC的距离等于2OH,即可求解.
解答 解:因为OA=OC,D是AC的中点,所以AC⊥OD,
又PO⊥底面⊙O,AC?底面⊙O,
所以AC⊥PO,而OD,PO是平面内的两条相交直线
所以AC⊥平面POD,又AC?平面PAC
所以平面POD⊥平面PAC
在平面POD中,过O作OH⊥PD于H,则OH⊥平面PAC
在Rt△ODA中,OD=DA•sin30=$\frac{1}{2}$
在Rt△POD中,OH=$\frac{\sqrt{2}×\frac{1}{2}}{\sqrt{2+\frac{1}{4}}}=\frac{\sqrt{2}}{3}$,
点B到平面PAC的距离等于2OH=$\frac{2\sqrt{2}}{3}$.
故选;B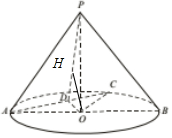
点评 题主要考查了直线与平面垂直的判定定理的应用,空间距离的求解,考查了运算推理的能力及空间想象的能力.属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π) 的图象如图所示,则ω=$\frac{3}{2}$;φ=$-\frac{π}{2}$.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π) 的图象如图所示,则ω=$\frac{3}{2}$;φ=$-\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2) | C. | [0,1] | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 质量指标值m | m<185 | 185≤m<205 | m≥205 |
| 等级 | 三等品 | 二等品 | 一等品 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com