练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．如果一个三位正整数如“a1a2a3”满足a1＜a2＞a3，则称这样的三位数为凸数（如120，232，354等），那么所有小于700的凸数的个数为（　　）
    A．44B．86C．112D．214

    分析 按照中间一个数字的情况分8类，当中间数为2时，百位数字只能选1，个位数字可以选1和0，当中间数为3时，百位数字有两种选择，个位数字有3种选择，以此类推，写出其他情况，利用加法原理得到结果．

    解答 解：按照中间一个数字的情况分8类，
    当中间数为2时，百位数字只能选1，个位数字可以选1和0，有1×2=2种；
    当中间数为3时，百位数字有两种选择，个位数字有3种选择，有2×3=6种；
    以此类推
    当中间数为4时，有3×4=12种；
    当中间数为5时，有4×5=20种；
    当中间数为6时，有5×6=30种；
    当中间数为7时，有6×7=42种；
    当中间数为8时，首位只有6种选择，末尾有8种选择，故有6×8=48种，
    当中间数为9时，首位只有6种选择，末尾有9种选择，故有6×9=54种，
    根据分类计数原理知故共有2+6+12+20+30+42+48+54=214种．
    故选：D．

    点评 数字问题是排列中的一大类问题，条件变换多样，把排列问题包含在数字问题中，解题的关键是看清题目的实质，很多题目要分类讨论，要做到不重不漏．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．函数g（x）=2cos（x-$\frac{π}{4}$）cos（x+$\frac{π}{4}$）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变）后得到h（x）的图象，设f（x）=$\frac{1}{4}$x2+h（x），则f′（x）的图象大致为（　　）
    A．B．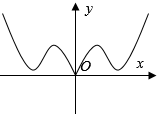
    C．D．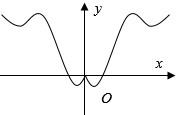

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知α是锐角，$sinα=\frac{3}{5}，则tanα$=（　　）
    A．$\frac{4}{5}$B．$\frac{3}{4}$C．$\frac{4}{3}$D．$\frac{5}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知a，b，c是正实数，则“b≤$\sqrt{ac}$”是“a+c≥2b”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设f″（x）是函数y=f（x）的导函数f′（x）的导数，定义：若f（x）=ax3+bx2+cx+d（a≠0），且方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的对称中心．有同学发现“任何一个三次函数都有对称中心”，请你运用这一发现处理下列问题：
    设$g（x）=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x+\frac{1}{12}$，则$g（\frac{1}{2016}）+g（\frac{2}{2016}）+g（\frac{3}{2016}）+…+g（\frac{2015}{2016}）$=2015．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列函数中既是奇函数，又在区间（0，+∞）内是增函数的为（　　）
    A．y=sinx，x∈RB．y=ln|x|，x∈R，且x≠0C．y=x3，x∈RD．y=x2，x∈R

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．曲线y=x2-1在点（1，0）处的切线方程为（　　）
    A．y=x-1B．y=-x+1C．y=2x-2D．y=-2x+2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．方程$\left\{\begin{array}{l}{x=1+sinθ}\\{y=sin2θ}\end{array}\right.$（θ是参数）所表示曲线经过下列点中的（　　）
    A．（1，1）B．（$\frac{2}{3}$，$\frac{1}{2}$）C．（$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$）D．（$\frac{2+\sqrt{3}}{2}$，-$\frac{1}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．sin（$\frac{π}{6}$+$\frac{2π}{3}$）=sin$\frac{π}{6}$是否成立？如果成立，能否说$\frac{2π}{3}$是函数y=sinx的周期？为什么？

    查看答案和解析>>

    同步练习册答案