
 已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$.
已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$. 分析 由题意知第m-1的最后一个数是数列{an}的第(m-1)2项,故A(9,13)是数列{an}的第82+13=77项,代入通项公式,可得答案.
解答 解:由题意知第一行的最后一个数字是数列{an}的第1项,
第二行的最后一个数字是数列{an}的第4项,
第三行的最后一个数字是数列{an}的第9项,
∴第m-1的最后一个数是数列{an}的第(m-1)2项,
∴A(9,13)是数列{an}的第82+13=77项;
∵an=$\frac{n}{2015}$,
∴A(9,13)=a77=$\frac{77}{2015}$,
故答案为:$\frac{77}{2015}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:解答题
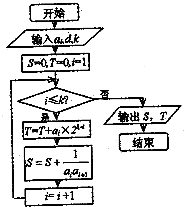 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com