
| x | 80 | 75 | 70 | 65 | 60 |
| y | 70 | 66 | 68 | 64 | 62 |
分析 (1)求出$\overline{x},\overline{y}$,代入回归系数公式求出$\stackrel{∧}{b}$,$\stackrel{∧}{a}$;
(2)将x=90代入回归方程求出$\stackrel{∧}{y}$.
解答 解:(1)$\overline{x}$=$\frac{1}{5}$(80+75+70+65+60)=70,$\overline{y}$=$\frac{1}{5}$(70+66+68+64+62)=66.
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=80×70+75×66+70×68+65×64+60×62=23190,
$\sum_{i=1}^{5}{{x}_{i}}^{2}$=802+752+702+652+602=24750,
∴$\stackrel{∧}{b}$=$\frac{23190-5×70×66}{24750-5×7{0}^{2}}$=0.36,$\stackrel{∧}{a}$=66-0.36×70=40.8.
∴线性回归方程为$\stackrel{∧}{y}$=0.36x+40.8.
(2)当x=90时,$\stackrel{∧}{y}$=0.36×90+40.8≈73,
答:预测学生F的物理成绩为73分.
点评 本题考查了线性回归方程的求解,代入公式正确计算是关键,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|0<x≤1} | C. | {x|-1≤x≤0} | D. | {x|x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}a$ | B. | $\frac{{\sqrt{6}}}{4}a$ | C. | $\frac{{\sqrt{6}}}{12}a$ | D. | $\frac{{\sqrt{3}}}{2}a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或-2 | B. | 0或2 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
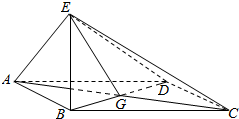 如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{18}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com