
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 设P(x0,y0),则Q(x0,-y0),y02=b2($\frac{{{x}_{0}}^{2}}{{a}^{2}}$-1).A(-a,0),B(a,0),利用斜率计算公式得到:λμ=-$\frac{{b}^{2}}{{a}^{2}}$,运用基本不等式求得最大值,注意等号成立的条件,再由离心率公式即可得出.
解答 解:设P(x0,y0),则Q(x0,-y0),y02=b2($\frac{{{x}_{0}}^{2}}{{a}^{2}}$-1),
即有$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,
由双曲线的方程可得A(-a,0),B(a,0),
则λ=$\frac{{y}_{0}}{{x}_{0}+a}$,μ=$\frac{{y}_{0}}{a-{x}_{0}}$,
∴λμ=$\frac{{{y}_{0}}^{2}}{{a}^{2}-{{x}_{0}}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$,
$\frac{16}{λμ}$+λμ=-[(-$\frac{16}{λμ}$)+(-λμ)]≤-2$\sqrt{\frac{16}{-λμ}•(-λμ)}$=-8,
当且仅当λμ=-4,即有b=2a,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a,
可得离心率e=$\frac{c}{a}$=$\sqrt{5}$.
故选:A.
点评 本题考查了双曲线的标准方程及其性质,考查直线的斜率公式,利用基本不等式求最值,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
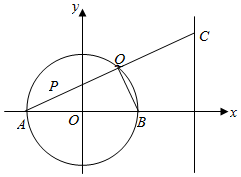 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
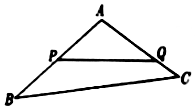 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
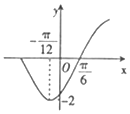 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com