
在平面直角坐标系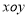 中,曲线
中,曲线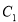 的参数方程为
的参数方程为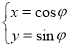 (
( 为参数),曲线
为参数),曲线 的参数方程为
的参数方程为 为参数),在以
为参数),在以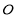 为极点,
为极点,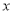 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线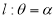 与
与 各有一个交点.当
各有一个交点.当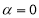 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明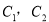 是什么曲线,并求出
是什么曲线,并求出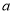 与
与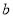 的值;
的值;
(2)设当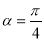 时,
时,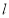 与
与 的交点分别为
的交点分别为 ,当
,当 时,
时,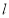 与
与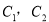 的交点为
的交点为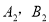 ,求四边形
,求四边形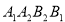 的面积.
的面积.
(1)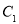 为圆,
为圆,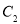 为椭圆,
为椭圆,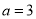 ,
,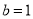 ;(2)四边形
;(2)四边形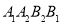 的面积为
的面积为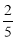
【解析】
试题分析:(1)将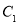 的参数方程化为普通方程可得
的参数方程化为普通方程可得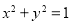 可知为圆方程,同理,将
可知为圆方程,同理,将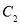 的参数方程化为普通方程可得
的参数方程化为普通方程可得 ,可知为椭圆方程,当
,可知为椭圆方程,当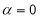 时,射线
时,射线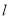 与
与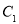 ,
,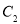 交点的直角坐标分别是
交点的直角坐标分别是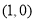 ,
,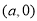 ,∵这两点间的距离为
,∵这两点间的距离为 ,∴
,∴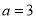 ,当
,当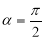 时,射线
时,射线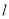 与
与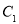 ,
,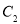 交点的直角坐标分别是
交点的直角坐标分别是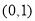 ,
,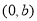 ,∵这两点重合,∴
,∵这两点重合,∴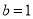 ;(2)根据题意可得当
;(2)根据题意可得当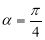 时,射线
时,射线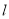 与
与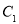 交点
交点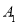 的横坐标是
的横坐标是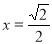 ,与
,与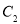 交点
交点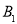 的横坐标是
的横坐标是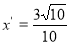 ;
;
当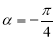 时,射线
时,射线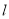 与
与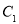 ,
,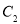 的两个交点
的两个交点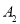 ,
,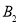 的分别与
的分别与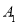 ,
,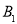 关于
关于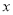 轴对称,易证四边形与
轴对称,易证四边形与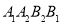 为梯形,∴四边形
为梯形,∴四边形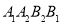 的面积为
的面积为 .
.
试题解析:(1)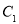 为圆,
为圆,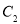 为椭圆,
为椭圆,
当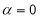 时,射线
时,射线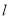 与
与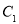 ,
,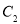 交点的直角坐标分别是
交点的直角坐标分别是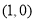 ,
,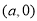 ,∵这两点间的距离为
,∵这两点间的距离为 ,∴
,∴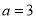 ,
,
当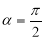 时,射线
时,射线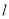 与
与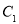 ,
,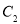 交点的直角坐标分别是
交点的直角坐标分别是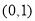 ,
,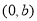 ,∵这两点重合,∴
,∵这两点重合,∴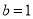 ;
;
(2)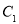 ,
,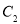 的普通方程分别为
的普通方程分别为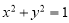 ,
,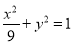 ,
,
当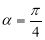 时,射线
时,射线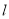 与
与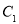 交点
交点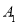 的横坐标是
的横坐标是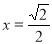 ,与
,与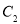 交点
交点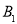 的横坐标是
的横坐标是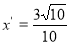 ;
;
当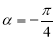 时,射线
时,射线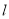 与
与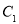 ,
,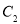 的两个交点
的两个交点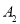 ,
,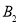 的分别与
的分别与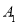 ,
,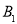 关于
关于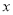 轴对称,∴四边形与
轴对称,∴四边形与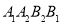 为梯形,∴四边形
为梯形,∴四边形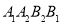 的面积为
的面积为 .
.
考点:1.参数方程化为普通方程;2.圆与圆锥曲线的综合.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届安徽省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
形如45132的数称为“波浪数”,即十位数字,千位数字均比与它们各自相邻的数字大,则由1,2,3,4,5可构成不重复的五位“波浪数”的个数为________.
查看答案和解析>>
科目:高中数学 来源:2015届宁夏银川市高三9月月考文科数学试卷(解析版) 题型:选择题
已知函数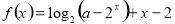 ,若
,若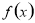 存在零点,则实数
存在零点,则实数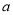 的取值范围是( )
的取值范围是( )
A.(-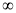 ,-4
,-4 ∪[4,+
∪[4,+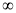
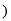 B.[1.+
B.[1.+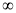

C.[2, +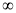
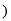 D.[4, +
D.[4, +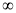

查看答案和解析>>
科目:高中数学 来源:2015届宁夏高三上学期第二次月考试卷理科数学试卷(解析版) 题型:解答题
已知函数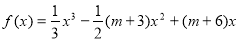 ,
,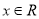 .(其中
.(其中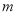 为常数)
为常数)
(1)当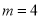 时,求函数的极值点和极值;
时,求函数的极值点和极值;
(2)若函数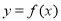 在区间
在区间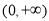 上有两个极值点,求实数
上有两个极值点,求实数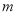 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com