
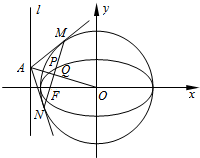
 在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.
在平面直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,左准线为l.P为椭圆C上任意一点,直线OQ⊥FP,垂足为Q,直线OQ与l交于点A.分析 (1)(i)将b=1代入椭圆的方程,根据椭圆的性质从而求出b,c;(ii)设P(m,n),表示出P点的坐标,根据FP、FQ的关系从而得到答案;
(2)设出M(x0,y0),表示出A(-$\frac{{a}^{2}}{c}$,t),求出$\overrightarrow{FM}$,$\overrightarrow{OA}$的坐标,由$\overrightarrow{FM}$•$\overrightarrow{OA}$=0,求出t,得到$\overrightarrow{AM}$•$\overrightarrow{OM}$的表达式,从而证出结论.
解答  解:(1)(i)由题意,b=1,$\frac{{a}^{2}}{c}$=$\frac{5}{2}$,又a2=b2+c2,
解:(1)(i)由题意,b=1,$\frac{{a}^{2}}{c}$=$\frac{5}{2}$,又a2=b2+c2,
所以2c2-5c+2=0,解得c=2,或c=$\frac{1}{2}$(舍去).故a2=5.
所求椭圆的方程为$\frac{{x}^{2}}{5}$+y2=1.
(ii)设P(m,n),则$\frac{{m}^{2}}{5}$+n2=1,即n2=1-$\frac{{m}^{2}}{5}$.
当m=-2,或n=0时,均不符合题意;
当m≠-2,n≠0时,直线FP的斜率为$\frac{n}{m+2}$,
直线FP的方程为y=$\frac{n}{m+2}$ (x+2).
故直线AO的方程为y=-$\frac{m+2}{n}$x,
Q点的纵坐标yQ=$\frac{2n(m+2)}{{(m+2)}^{2}{+n}^{2}}$,
所以$\frac{FP}{FQ}$=|$\frac{n}{yP}$|=|$\frac{{(m+2)}^{2}{+n}^{2}}{2(m+2)}$|
=|$\frac{{4m}^{2}+20m+25}{10(m+2)}$|,
令$\frac{FP}{FQ}$=$\frac{1}{10}$,得4m2+21m+27=0 ①,或4m2+19m+23=0 ②,
由4m2+21m+27=0,解得m=-3,m=-$\frac{9}{4}$,
又-$\sqrt{5}$≤m≤$\sqrt{5}$,所以方程①无解.
由于△=192-4×4×23<0,所以方程②无解,
故不存在点P使$\frac{FP}{FQ}$=$\frac{1}{10}$.
(3)设M(x0,y0),A(-$\frac{{a}^{2}}{c}$,t),
则$\overrightarrow{FM}$=(x0+c,y0),$\overrightarrow{OA}$=(-$\frac{{a}^{2}}{c}$,t).
因为OA⊥FM,所以$\overrightarrow{FM}$•$\overrightarrow{OA}$=0,即(x0+c)(-$\frac{{a}^{2}}{c}$)+ty0=0,
由题意y0≠0,所以t=$\frac{{x}_{0}+c}{{y}_{0}}$•$\frac{{a}^{2}}{c}$.
所以A(-$\frac{{a}^{2}}{c}$,$\frac{{x}_{0}+c}{{y}_{0}}$•$\frac{{a}^{2}}{c}$).
因为$\overrightarrow{AM}$=(x0+$\frac{a2}{c}$,y0-$\frac{{x}_{0}+c}{{y}_{0}}$•$\frac{{a}^{2}}{c}$),$\overrightarrow{OM}$=(x0,y0),
所以$\overrightarrow{AM}$•$\overrightarrow{OM}$=(x0+$\frac{{a}^{2}}{c}$)x0+(y0-$\frac{{x}_{0}+c}{{y}_{0}}$•$\frac{{a}^{2}}{c}$)y0
=x02+y02+$\frac{{a}^{2}}{c}$x0-$\frac{{x}_{0}+c}{{y}_{0}}$•$\frac{{a}^{2}}{c}$y0
=x02+y02+$\frac{{a}^{2}}{c}$x0-$\frac{{a}^{2}}{c}$x0-a2
=x02+y02-a2.
因为M(x0,y0)在圆O上,所以$\overrightarrow{AM}$•$\overrightarrow{OM}$=0.
即AM⊥OM,所以直线AM与圆O相切.
同理可证直线AN与圆O相切.
点评 本题考察了直线和椭圆的关系,考察椭圆的方程问题,考察向量的应用,本题是一道难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,3] | C. | [2,4] | D. | [3,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com