练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
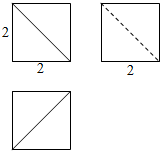
    5．棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示，则该几何体的表面积为（　　）
    A．$\frac{20}{3}$B．18C．$24+2\sqrt{3}$D．$18+2\sqrt{3}$

    分析 作出几何体的直观图，观察截去几何体的结构特征，代入数据计算．

    解答 解：由三视图可知正方体边长为2，截去部分为三棱锥，作出几何体的直观图如图所示：

    故该几何体的表面积为：3×22+3×（$\frac{1}{2}×{2}^{2}$）+$\frac{\sqrt{3}}{4}•（{2}^{2}+{2}^{2}）$=$18+2\sqrt{3}$，
    故选：D．

    点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

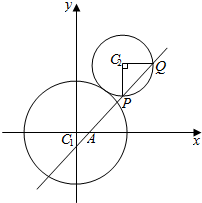    15．已知圆C1：x2+y2=9与圆C2：（x-3）2+（y-4）2=r2（r＞0）相外切．
    （1）若圆C2关于直线l：$\frac{ax}{9}$-$\frac{by}{12}$=1对称，求由点M（a，b）向圆C2所作的切线长的最小值；
    （2）若直线l1过点A（1，0），与圆C2相交于P、Q两点．且S${\;}_{△{C}_{2}PQ}$=2求此时直线l1的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

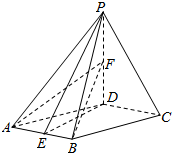    16．已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PA=AD，点E为AB中点，点F在线段PD上，且PF：FD=1：3．
    （1）证明平面PED⊥平面FAB；
    （2）若PD=4，求三棱锥P-FAB的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

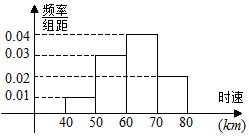
    13．400辆汽车通过某公路时，时速的频率分布直方图如图所示，则时速在[60，80）的汽车大约有（　　）
    A．120辆B．140辆C．160辆D．240辆

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

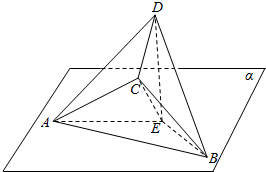    20．如图，三棱锥C-ABD的棱AB在平面α内，棱CD在平面α外，平面CAB⊥平面α，点D在平面α内的射影为E，且满足EA⊥EB，AC=BC=EA=EB=2，DE=2$\sqrt{2}$．
    （1）求证：AE∥平面BCD；
    （2）求二面角E-CD-B的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知命题p：x≤1，命题q：$\frac{1}{x}$≥1，则命题p是命题q的必要不充分条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，$\overline{x_1}$，$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数，$S_1^2$，$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差，则有（　　）
    A．$\overline{x_1}$＞$\overline{x{\;}_2}$，$S_1^2$＜$S_2^2$B．$\overline{x_1}$=$\overline{x{\;}_2}$，$S_1^2$＞$S_2^2$
    C．$\overline{x_1}$=$\overline{x{\;}_2}$，$S_1^2$=$S_2^2$D．$\overline{x_1}$=$\overline{x{\;}_2}$，$S_1^2$＜$S_2^2$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．当x＞0时，证明不等式1n（1+x）＞x-$\frac{1}{2}$x2成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．有四个命题：①若$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$，则$\overrightarrow{p}$与$\overrightarrow{a}$、$\overrightarrow{b}$共面；②若$\overrightarrow{p}$与$\overrightarrow{a}$、$\overrightarrow{b}$共面，则$\overrightarrow{p}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$；③若$\overrightarrow{MP}$=x$\overrightarrow{MA}$+y$\overrightarrow{MB}$，则P，M，A，B共面；④若P，M，A，B共面，则$\overrightarrow{MP}$=x$\overrightarrow{MA}$+y$\overrightarrow{MB}$．其中真命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案