
分析 (1)由余弦定理化简已知可得a2=c2+b2-bc,根据余弦定理可求cosA,结合范围A∈(0,π),即可解得A的值.
(2)利用三角函数恒等变换的应用化简可得sinB+sinC=$\sqrt{3}$sin(B+$\frac{π}{6}$),结合范围B∈(0,$\frac{2π}{3}$),可求B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),利用正弦函数的性质即可解得sinB+sinC的取值范围.
解答 (本小题满分12分)
解:(1)∵$c({acosB-\frac{1}{2}b})={a^2}-{b^2}$,
由余弦定理得:a2+c2-b2-bc=2a2-2b2,可得:a2=c2+b2-bc,…3分
∵a2=c2+b2-2bccosA,
∴cosA=$\frac{1}{2}$,…5分
∵A∈(0,π),
∴$A=\frac{π}{3}$. …(6分)
(2)sinB+sinC=sinB+sin(A+B)=sinB+sinAcosB+cosAsinB…(7分)
=$\frac{3}{2}sinB+\frac{{\sqrt{3}}}{2}cosB=\sqrt{3}sin({B+\frac{π}{6}})$; …(9分)
∵$B∈({0,\frac{2π}{3}})$,
∴$B+\frac{π}{6}∈({\frac{π}{6},\frac{5π}{6}})$,$sin({B+\frac{π}{6}})∈({\frac{1}{2},1}]$. …(11分)
∴sinB+sinC的取值范围为($\frac{{\sqrt{3}}}{2}$,$\sqrt{3}$]. …(12分)
点评 本题主要考查了余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想和数形结合思想的应用,考查了计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
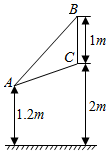 如图,化工厂的主控制表盘高BC=1米,表盘底边距地面2米,设值班人员坐在椅子上时,眼睛距地面1.2米,问值班人员坐在什么位置上看表盘效果最佳?(即视角∠BAC最大)
如图,化工厂的主控制表盘高BC=1米,表盘底边距地面2米,设值班人员坐在椅子上时,眼睛距地面1.2米,问值班人员坐在什么位置上看表盘效果最佳?(即视角∠BAC最大)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
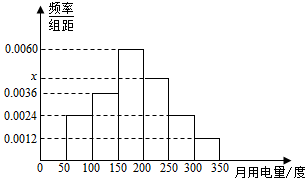 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为52.
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为52.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100海里 | B. | 100$\sqrt{2}$海里 | C. | 100$\sqrt{3}$海里 | D. | 200海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
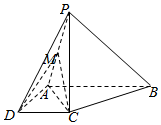 如图,在四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.
如图,在四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com