
分析 (I)分类讨论,当0<x≤2时,由|log2x|=1;当2<x≤10时,由$sin\frac{πx}{4}=1$,即可求函数g(x)的零点;
(II)画出函数f(x)的图象,确定x1x2=1,x3+x4=12,2<x3<x4<10,由此可得则$\frac{{({{x_3}-1})({{x_4}-1})}}{{{x_1}•{x_2}}}$的取值范围.
解答 (本题满分为12分)
解:(Ⅰ)当0<x≤2时,由|log2x|=1解得x=2或$x=\frac{1}{2}$;
当2<x≤10时,由$sin\frac{πx}{4}=1$解得x=10,
∴函数g(x)有3个零点,分别为x=2,$x=\frac{1}{2}或x=10$.…(4分)
(Ⅱ)设f(x1)=f(x2)=f(x3)=f(x4)=a,由题意可知函数f(x)的图象与直线y=a交于四个不同的点.
在同一坐标系内作出两个函数的图象: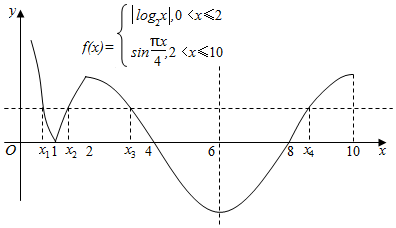
结合图象,由题意可知,x3+x4=12;…(7分)
由|log2x1|=|log2x2|知,-log2x1=log2x2,即x1•x2=1.…(9分)
若函数f(x)的图象与直线y=a图象始终有四个交点,则2<x3<4.…(10分)
故$\frac{{({{x_3}-1})({{x_4}-1})}}{{{x_1}•{x_2}}}=({{x_3}-1})({11-{x_3}})=-{({{x_3}-6})^2}+25$…(11分)
因2<x3<4,所以,$9<-{({{x_3}-6})^2}+25<21$.
所以,$\frac{{({{x_3}-1})({{x_4}-1})}}{{{x_1}•{x_2}}}$的取值范围为(9,21).…(12分)
点评 本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{10}{11}$ | B. | $\frac{5}{6}$ | C. | $\frac{5}{11}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次解题比赛中,甲、乙两组各四名同学答对题目数如茎叶图.
在一次解题比赛中,甲、乙两组各四名同学答对题目数如茎叶图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com