
���� ��1���ǡ�����Ϊ���㡱Ϊ�¼�A�����ҿ���Ϊ���㡱Ϊ�¼�B����������Ϊ���㡱Ϊ�¼�C�����ס��ҡ���������һ������Ϊ���㡱Ϊ�¼�D���ɴ�����P��D��=1-P��$\overline{A}\overline{B}\overline{C}$�������������ο����У�־Ը�ס��ҡ���������������һ������Ϊ����ĸ��ʣ�
��2�������⣬��X�Ŀ���ȡֵ��3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ�������������X�ķֲ��к���ѧ������
��� �⣺��1���ǡ�����Ϊ���㡱Ϊ�¼�A�����ҿ���Ϊ���㡱Ϊ�¼�B��
��������Ϊ���㡱Ϊ�¼�C�����ס��ҡ���������һ������Ϊ���㡱Ϊ�¼�D��
��P��D��=1-P��$\overline{A}\overline{B}\overline{C}$��=1-P��$\overline{A}$��P��$\overline{B}$��P��$\overline{C}$��
=1-$\frac{1}{5}��\frac{1}{3}��\frac{1}{3}$
=$\frac{44}{45}$��
��2�������⣬��X�Ŀ���ȡֵ��3��4��5��6��
��ΪP��X=3��=P��$\overline{A}\overline{B}\overline{C}$��=P��$\overline{A}$��P��$\overline{B}$��P��$\overline{C}$��=$\frac{1}{45}$��
P��X=4��=P��A$\overline{B}$$\overline{C}$��+P��$\overline{A}B\overline{C}$��+P��$\overline{A}\overline{B}C$��=$\frac{8}{45}$��
P��X=5��=P��$\overline{A}BC$��+P��A$\overline{B}$C��+P��AB$\overline{C}$��=$\frac{4}{9}$��
P��X=6��=P��ABC��=P��A��P��B��P��C��=$\frac{16}{45}$��
����X�ķֲ���Ϊ��
| X | 3 | 4 | 5 | 6 |
| P | $\frac{1}{45}$ | $\frac{8}{45}$ | $\frac{4}{9}$ | $\frac{16}{45}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��С���ѧ�����������е��⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{5}$ | B�� | 41 | C�� | 21 | D�� | 20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
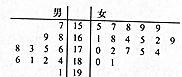 ij���жԳ����꼶��ѧ���������ʲ��ԣ���֪����һ���ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ���£���λ��cm����
ij���жԳ����꼶��ѧ���������ʲ��ԣ���֪����һ���ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ���£���λ��cm�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\frac{5}{4}$ | C�� | $\frac{5}{4}$��2 | D�� | $\sqrt{2}$��$\frac{{\sqrt{5}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��0] | B�� | ��-$\frac{3}{4}$-ln2��1] | C�� | ��-$\frac{3}{4}$-ln2��+�ޣ� | D�� | ��-�ޣ�-$\frac{3}{4}$-ln2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������S-ABCD�ĵ����ı���ABCDΪƽ���ı��Σ�����AC��BD����AC��BD�ཻ��O����SBC=��SBA��
��ͼ��ʾ������S-ABCD�ĵ����ı���ABCDΪƽ���ı��Σ�����AC��BD����AC��BD�ཻ��O����SBC=��SBA���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com