Question

8．在如图所示的多面体BACDE中，AB⊥平面ACD，DE⊥平面ACD，且AC=AD=CD=DE=2，AB=1
（1）已知M、N分别为AD、BE的中点，证明：AD⊥平面CMN；
（2）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一结论．

Answer 1

分析 （1）先证明AD⊥CM，再结合已知证明AD⊥MN，又MN∩CM=M，即可由判定定理可证AD⊥平面MNC．
（2）分别取CE、CD的中点F、H，连接BF、FH、AH，利用三角形的中位线定理和平行四边形的判定定理及线面平行的判定定理即可证明．

解答 解：（1）∵AC=AD=CD，M为AD的中点，可得AD⊥CM，
∵AB⊥平面ACD，DE⊥平面ACD，M、N分别为AD、BE的中点，可得AD⊥MN，
又∵MN∩CM=M，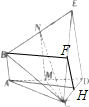
∴AD⊥平面MNC．
（2）由已知AB⊥平面ACD，DE⊥平面ACD，∴AB∥ED，
设F为线段CE的中点，H是线段CD的中点，
连接FH，则FH∥=$\frac{1}{2}$ED，∴FH∥=AB，
∴四边形ABFH是平行四边形，∴BF∥AH，
由BF?平面ACD内，AH?平面ACD，
∴BF∥平面ACD．

点评 本题主要考查了直线与平面平行的判定，直线与平面垂直的判定，解题的关键是利用三角形的中位线定理、平行四边形的判定定理及线面平行的判定定理，属于中档题．