
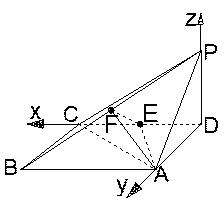
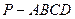 中,底面
中,底面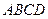 为矩形,
为矩形,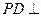 底面
底面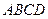 ,
,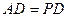 ,
,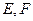 分别为
分别为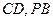 的中点
的中点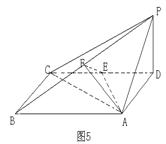
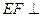 面
面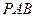 ;
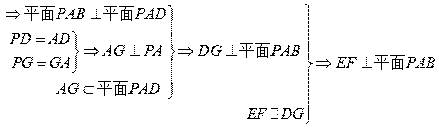
; ,求
,求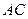 与面
与面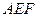 所成角的余弦值
所成角的余弦值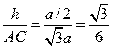

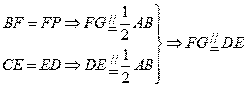
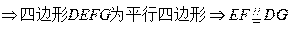
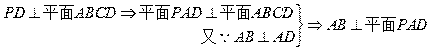
 ……(6分)
……(6分)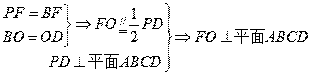
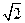 a, ∴PA=
a, ∴PA=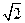 a, DG=
a, DG=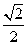 a=EF, ∴PB=2a, AF=a.
a=EF, ∴PB=2a, AF=a.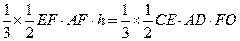
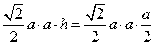 ∴
∴
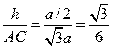 .
.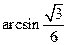 …(12分)
…(12分)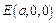 ,其中
,其中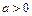 ,则
,则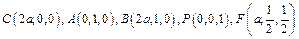 ,
,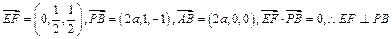 ,
,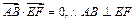
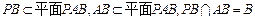 ,
,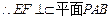 …(6分)
…(6分)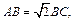 得
得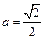 ,
,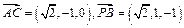
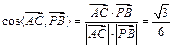 ,
,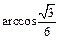 ,
,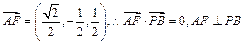 ,
,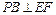 ,AF为平面AEF内两条相交直线,
,AF为平面AEF内两条相交直线, ,
,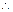 AC与平面AEF所成的角为
AC与平面AEF所成的角为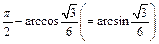 ,
,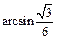 …(12分)
…(12分)

 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
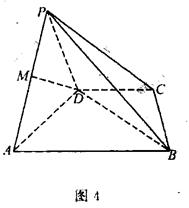
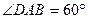 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面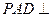 底面ABCD,且
底面ABCD,且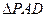 为等腰直角三角形,
为等腰直角三角形,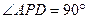 ,M为AP的中点。
,M为AP的中点。 (1)求证:
(1)求证: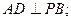
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
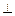 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM PBD.
PBD.
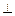 平面AMD
平面AMD 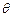 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
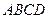 是边长为
是边长为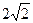 的正方形,
的正方形,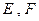 分别为
分别为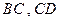 的中点,沿
的中点,沿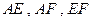 将
将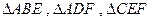 向同侧折叠且与平面
向同侧折叠且与平面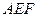 成直二面角,连接
成直二面角,连接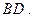
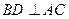 ;
;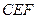 与平面
与平面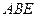 所成锐角的余弦值。
所成锐角的余弦值。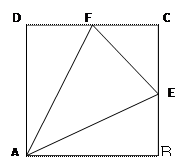

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
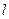 ⊥平面
⊥平面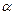 内所有直线”的充要条件是“
内所有直线”的充要条件是“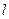 ⊥平面
⊥平面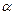 ”;
”;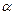 ∥平面
∥平面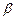 ”的必要不充分条件是“
”的必要不充分条件是“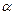 内存在不共线三点到
内存在不共线三点到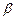 的距离相等”;
的距离相等”;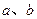 是异面直线,
是异面直线,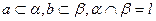 则
则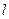 至少与
至少与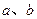 中的一条相交.
中的一条相交.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4
个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4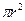 ) ( )
) ( )A.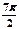 | B.14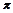 | C.56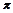 | D.96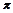 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
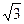 的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.
的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.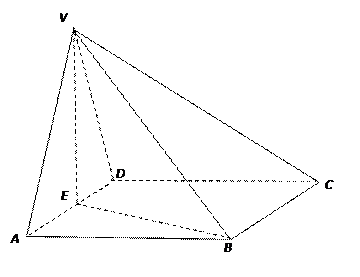 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com