
分析 (1)据题意,G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=$\sqrt{6}$,半焦距c=$\sqrt{3}$,即可得到椭圆方程;
(2)据题意,四边形OASB为矩形即$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即x1x2+y1y2=0.设出直线方程,将直线方程与椭圆方程联立,据韦达定理表示出则x1x2+y1y2=0,解方程求出参数,即得到直线方程.
解答 解:(1)由$\overrightarrow{NP}$=-2$\overrightarrow{PQ}$,$\overrightarrow{CQ}$•$\overrightarrow{NP}$=0,可得Q为PN的中点且GQ⊥PN,
∴GQ为PN的中垂线,
∴|PG|=|GN|
∴|GN|+|GM|=|MP|=2$\sqrt{6}$,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长a=$\sqrt{6}$,半焦距c=$\sqrt{3}$,
∴短半轴长b=$\sqrt{3}$,
∴点G的轨迹方程是$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$---------(6分)
(2)因为$\overrightarrow{OS}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,所以四边形OASB为平行四边形
若存在l使得|$\overrightarrow{OS}$|=|$\overrightarrow{AB}$|,则四边形OASB为矩形,∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0
若l的斜率不存在,直线l的方程为x=2,则A(2,1),B(2,-1)
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=3与$\overrightarrow{OA}$•$\overrightarrow{OB}$=0矛盾,故l的斜率存在.
设l的方程为y=k(x-2),A(x1,y1),B(x2,y2),
代入椭圆方程可得(2k2+1)x2-8k2x+8k2-6=0,
∴x1+x2=$\frac{8{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{8{k}^{2}-6}{2{k}^{2}+1}$,
∴y1y2=k(x1-2)•k(x2-2)=-$\frac{2{k}^{2}}{2{k}^{2}+1}$
∴x1x2+y1y2=$\frac{8{k}^{2}-6}{2{k}^{2}+1}$-$\frac{2{k}^{2}}{2{k}^{2}+1}$=0,
∴k=±1
∴存在直线x-y-2=0或x+y-2=0使得四边形OASB的对角线相等.---------(14分)
点评 本题考查椭圆方程的求法;考查直线与椭圆的位置关系,解决的关键是将已知转化为x1x2+y1y2=0,属于一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
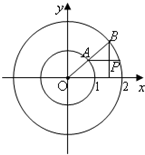 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
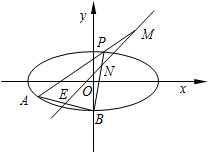 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
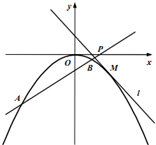 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {$\sqrt{2}$} | B. | {2} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {-2,1,$\sqrt{2}$,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com