
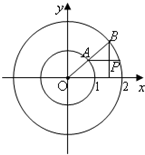
 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)分析 (Ⅰ)由A(cosx,sinx),P(2cosx,sinx),根据三角函数中的恒等变换应用可得,f(x)=2sin(2x+$\frac{π}{6}$)+2,即可得解f(x)的最值;
(Ⅱ)由-$\frac{π}{2}$+2k$π≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$(k∈Z)得f(x)的单调增区间.同理可得f(x)的单调减区间,对称中心.
解答 (本题满分12分)
解:(Ⅰ) 依题意,A(cosx,sinx),P(2cosx,sinx),
$\overrightarrow{OA}$•$\overrightarrow{OP}$=2cos2x+sin2x=1+cos2x,
因此,f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
=1+cos2x+cos2x+2$\sqrt{3}$sinxcosx
=1+2cos2x+$\sqrt{3}$sin2x+cos2x+2
=2sin(2x+$\frac{π}{6}$)+2
所以,f(x)的最大值为4,最小值为0; …(6分)
(Ⅱ)由-$\frac{π}{2}$+2k$π≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$(k∈Z)得:-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}+kπ$(k∈Z),
因此,f(x)的单调增区间为:[-$\frac{π}{3}$+kπ,$\frac{π}{6}+kπ$](k∈Z),
同理可得:f(x)的单调减区间为[$\frac{π}{6}$+kπ,$\frac{2π}{3}+kπ$](k∈Z),
其图象的对称中心为(-$\frac{π}{12}$+$\frac{kπ}{2}$,2)(k∈Z) …(12分)
点评 本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{470+10\sqrt{30}}}{3}$ | B. | 175 | C. | 180 | D. | 295+10$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com