练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．曲线y=2x-x3在点（1，1）处的切线方程为x+y-2=0．

    分析 根据导数的几何意义求出函数在x=1处的导数，从而得到切线的斜率，再利用点斜式方程写出切线方程即可．

    解答 解：y=2x-x3的导数为y'=2-3x2
    即有在点（1，1）处的切线斜率为k=y'|x=1=-1，
    而切点的坐标为（1，1），
    ∴曲线y=2x-x3在x=1的处的切线方程为y-1=-（x-1），
    即为x+y-2=0．
    故答案为：x+y-2=0．

    点评 本题主要考查了利用导数研究曲线上某点切线方程，考查运算求解能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

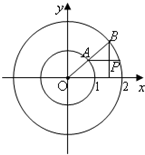    15．如图所示，射线OA与单位圆交于A，与圆x2+y2=4交于点B，过A平行于x轴的直线与过B与x轴垂直的直线交于P点，OA与x轴的夹角为x，若f（x）=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx（cosx+2$\sqrt{3}$sinx）
    （Ⅰ）求f（x）的最值；
    （Ⅱ）求f（x）的单调区间和图象的对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列四个命题中：
    ①从匀速传递的产品生产流水线上，质检员每10分钟抽取一件产品进行某项指标检测，这样的抽样是分层抽样．
    ②我们经常利用相关指数R2来刻画回归模型的拟合效果，R2的值越大，说明回归模型的拟合效果越好；
    ③在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0），若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）取值的概率为0.8；
    ④在两个分类变量的独立性检验中，若分类变量X与Y的K2观测值k0为0.4，判断“X与Y有关系”的把握程度越大．
    其中真命题的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知集合A={x|x2=2}，B={1，$\sqrt{2}$，2}，则A∩B=（　　）
    A．{$\sqrt{2}$}B．{2}C．{-$\sqrt{2}$，1，$\sqrt{2}$，2}D．{-2，1，$\sqrt{2}$，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知b是a、c的等差中项，lg（b-5）是lg（a-1）与lg（c-6）的等差中项，又a，b，c三数之和为33，求这三个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某考生参加一种测试，需回答三个问题，规定：每题回答正确得100分，回答不正确得-100分．已知该考生每题回答正确的概率都是0.8，且各题回答正确与否相互之间没有影响．
    （1）求这名同学回答这三个问题的总得分X的概率分布列和数学期望；
    （2）求这名同学总得分不低于100分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．如图，一隧道截面由一个长方形和抛物线构成，现欲在隧道抛物线拱顶上安装交通信息采集装置，若位置C对隧道底AB的张角θ最大时采集效果最好，则采集效果最好时位置C到AB的距离是（　　）
    A．2$\sqrt{2}$mB．2$\sqrt{3}$mC．4mD．6m

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知cn=（3n-1）$\frac{2}{{3}^{n}}$，n=1，2，3，…，Tn为数列{cn}的前n项和，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知定义在R上的函数φ（x）与g（x）满足：φ（x）+g（x）=ex-x2-2x-2，φ（x）-g（x）=ex+x2+2x-4；（注：e为自然对数的底数，e≈2.78）；
    （1）求φ（x），g（x）的解析式；
    （2）对?x1∈[-1，1]，?x2∈[0，1]，都有g（x1）+ax1+5≥φ（x2）-x2φ（x2）成立，求实数a的范围；
    （3）设f（x）=$\left\{\begin{array}{l}{φ（x），（x＞0）}\\{g（x），（x≤0）}\end{array}\right.$，判断方程f[f（x）]=2的解的个数，并说明理由．

    查看答案和解析>>

    同步练习册答案