
分析 (1)利用方程组法基本进行求解即可.
(2)将不等式恒成立转化为求h(x)min≥F(x)max,利用导数分别求出h(x)和F(x)的最小值和最大值,即可.
(3)利用数形结合,对参数进行讨论求出方程的根的个数
解答 解:(1)∵φ(x)+g(x)=ex-x2-2x-2,φ(x)-g(x)=ex+x2+2x-4;
∴解得φ(x)=ex-3,g(x)=-x2-2x+1;
(2)设h(x)=g(x)+ax+5=-x2+(a-2)x+6,
F(x)=φ(x)-xφ(x)=(1-x)(ex-3)=(1-x)ex+3x-3,
对?x1∈[-1,1],?x2∈[0,1],都有h(x)min≥F(x)max成立,
∵F′(x)=-xex+3在[0,1]上为减函数,
∴F′(x)min≥F′(1)=3-e>0,
∴F(x)在[0,1]上单调递增,
∴F(x)max=F(1)=0,
∴$\left\{\begin{array}{l}{h(-1)=7-a≥0}\\{h(1)=a+3≥0}\end{array}\right.$,解得-3≤a≤7,
∴实数a的取值范围为[-3,7].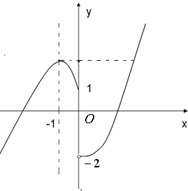
(3)当f(x)>0时,有ef(x)-3=2,则f(x)=ln5,
当f(x)≤0时,有f[f(x)]=-f(x)2-2f(x)+1=2,
则f(x)=-1,
即若f[f(x)]=2,则有f(x)=-1或f(x)=ln5,
而f(x)的图象如图所示:
y=f(x)与y=-1有2个交点,与y=ln5有1个交点,
则f[f(x)]=2共有3个解.
点评 本题主要考查函数解析式的方法,利用最值解决恒成立问题;利用数结合法解决方程根的个数问题.这是一道综合性很强的导数试题.难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
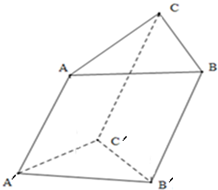 斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.
斜三棱柱底面边长是4cm的正三角形,.侧棱长3cm,侧棱∠AA′C′=∠AA′B′=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com