练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．某篮球架的底座三视图如图所示，则其体积为（　　）
    A．$\frac{{470+10\sqrt{30}}}{3}$B．175C．180D．295+10$\sqrt{2}$

    分析 由已知中的三视图，可知该几何体是一个以侧视图为底面的六棱柱，求出底面面积，代入棱柱体积公式，可得答案．

    解答 解：由已知中的三视图，可知该几何体是一个以侧视图为底面的六棱柱，
    底面面积S=1×6+$\frac{1}{2}$×（1+2）×1+2×5=17$\frac{1}{2}$，
    棱柱的高h=10，
    故棱柱的体积V=Sh=175，
    故选：B．

    点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．下列函数中，在其定义域内既是奇函数又是增函数的是（　　）
    A．y=tanxB．y=2xC．y=xD．y=lg（1+x2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥1}\\{y-2≤0}\end{array}\right.$，则目标函数z=3x+y的最大值为（　　）
    A．-1B．3C．11D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．5位男生与5位女生排成一排，男生甲与男生乙之间有且只有2位女生，女生不排在两端，这样的排列种数为（　　）
    A．5760B．57600C．2880D．28800

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

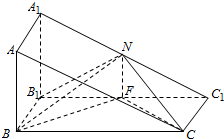    5．直三棱柱ABC-A1B1C1中，AB=BB1=$\frac{1}{2}$BC，∠ABC=90°，N、F分别是A1C1、B1C1的中点．
    （Ⅰ）求证：CF⊥平面NFB；
    （Ⅱ）求二面角C-BN-B1的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

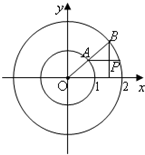    15．如图所示，射线OA与单位圆交于A，与圆x2+y2=4交于点B，过A平行于x轴的直线与过B与x轴垂直的直线交于P点，OA与x轴的夹角为x，若f（x）=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx（cosx+2$\sqrt{3}$sinx）
    （Ⅰ）求f（x）的最值；
    （Ⅱ）求f（x）的单调区间和图象的对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．光点随机出现在圆C1：4x2+4y2=π2的内部，则光点出现曲线C2：y2-cos2x=0，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]内部的概率为$\frac{16}{{π}^{3}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

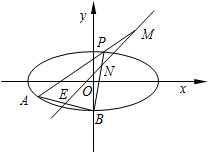    13．如图，已知椭圆$C：\frac{x^2}{12}+\frac{y^2}{4}=1$，点B是其下顶点，过点B的直线交椭圆C于另一点A（A点在x轴下方），且线段AB的中点E在直线y=x上．
    （1）求直线AB的方程；
    （2）若点P为椭圆C上异于A、B的动点，且直线AP，BP分别交直线y=x于点M、N，证明：OM•ON为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知b是a、c的等差中项，lg（b-5）是lg（a-1）与lg（c-6）的等差中项，又a，b，c三数之和为33，求这三个数．

    查看答案和解析>>

    同步练习册答案