
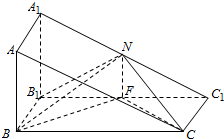
 直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.
直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.分析 (Ⅰ)根据直棱柱的性质及AB⊥BC,判定NF与平面BC1的垂直关系,再由线面垂直的性质判断线线垂直,然后由线线垂直⇒线面垂直;
(Ⅱ)连接B1G交BF于点O,过O作BN的垂线,垂足为M,∠B1MG的余弦值为二面角C-BN-B1的余弦值.
解答  (Ⅰ)证明:直三棱柱ABC-A1B1C1中,
(Ⅰ)证明:直三棱柱ABC-A1B1C1中,
B1B⊥AB,BC⊥AB,又B1B∩BC=B,
∴AB⊥平面BB1C1C.
又N、F分别为A1 C1、B1 C1的中点
∴AB∥A1B1∥NF.
∴NF⊥平面BB1C1C.
∵FC?平面BB1C1C,∴NF⊥FC.
取BC中点G,有BG=GF=GC,∴BF⊥FC,
又NF∩FB=F,
∴FC⊥平面NFB;
(Ⅱ)解:连接B1G交BF于点O,过O作BN的垂线,垂足为M,
∵FC⊥平面NFB,FC∥B1G,
∴B1G⊥平面NFB,
∵BN?平面NFB,
∴B1G⊥BN
∵MO⊥BN,
∴BN⊥平面B1GM,
∴B1M⊥BN,GM⊥BN,
∴∠B1MG的余弦值为二面角C-BN-B1的余弦值.
∵GB1⊥MO,BO=OG,
∴B1N=GM,
∴△B1MG为等腰三角形,
令AB=a,则B1G=$\sqrt{2}a$,MO=$\frac{1}{2}•\frac{BF×FN}{BN}$=$\frac{\sqrt{2}}{6}$a,
B1M=GM=$\sqrt{(\frac{1}{2}{B}_{1}G)^{2}+M{O}^{2}}$=$\frac{\sqrt{5}}{3}$a,
∴二面角C-BN-B1的余弦值=$\frac{{B}_{1}{M}^{2}+M{G}^{2}-{B}_{1}{G}^{2}}{2{B}_{1}M×MG}$=-$\frac{4}{5}$.
点评 本题考查线面垂直的判定,考查二面角C-BN-B1的余弦值,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{470+10\sqrt{30}}}{3}$ | B. | 175 | C. | 180 | D. | 295+10$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
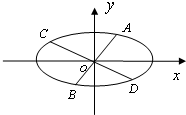 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com