
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
| |2| | ||
|
| 2 |
| c |
| a |
| ||
| 3 |
| 3 |
| x2 |
| 3 |
| y2 |
| 2 |
| 1 |
| 2 |
| x02 |
| 3 |
| y02 |
| 2 |
| 6 |
| 2+3k2 |
| 6k |
| 2+3k2 |
| 6 | ||
3k+
|
| 6 | ||||
2
|
| ||
| 2 |
| 2 |
| k |
| ||
| 3 |
| ||
| 2 |


科目:高中数学 来源: 题型:
| MA |
| MB |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 10001 |
| 10000 |
| 1001 |
| 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
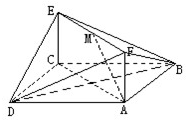 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:| 分数段(分) | [90,110) | [110,130) | [130,150] |
| 频数 | 4 | ||
| 频率 | a | 0.45 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com