
分析 (I)函数的定义域为{x|x≠0},直接利用奇偶性定义证明即可;
(II)直接利用函数单调性定义证明即可;
(III)根据函数的性质(I)(II)可直接得出结果;
解答 解:(I)由题意知:x≠0;
∴函数的定义域为{x|x≠0};
又∵$f(-x)=-x-\frac{1}{x}=-(x+\frac{1}{x})=-f(x)$;
∴函数f(x)为奇函数;
(II)设0<x1<x2<1则
$f({x_1})-f({x_2})={x_1}+\frac{1}{x_1}-{x_2}-\frac{1}{x_2}=({x_1}-{x_2})-\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}=({x_1}-{x_2})(1-\frac{1}{{{x_1}{x_2}}})$;
∵0<x1<x2<1;
∴${x_1}-{x_2}<0,1-\frac{1}{{{x_1}{x_2}}}<0$;
∴f(x1)-f(x2)>0即f(x1)>f(x2);
∴函数f(x)在(0,1)上是减函数;
(III)函数f(x)在(-1,0)上是减函数.
点评 本题主要考查了函数的奇偶性定义、单调性定义证明等函数基本性质,属基础题.


科目:高中数学 来源: 题型:选择题
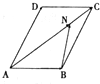
| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3或-1 | B. | 3 | C. | 1 | D. | -3或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{13}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$-3 | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com