
【题目】已知抛物线![]() (
(![]() ),直线
),直线![]() 与抛物线
与抛物线![]() 交于
交于![]() (点
(点![]() 在点
在点![]() 的左侧)两点,且
的左侧)两点,且![]() .
.
(1)求抛物线![]() 在
在![]() 两点处的切线方程;
两点处的切线方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且
两点,且![]() 的中点在线段
的中点在线段![]() 上,
上, ![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)第(1)问,先求出抛物线的方程![]() 得到
得到![]() ,再求导求出切线斜率,最后求出抛物线
,再求导求出切线斜率,最后求出抛物线![]() 在
在![]() 两点处的切线方程.(2)第(2)问,先利用弦长公式求出
两点处的切线方程.(2)第(2)问,先利用弦长公式求出![]() ,再利用点到直线的距离求三角形的高
,再利用点到直线的距离求三角形的高![]() ,最后写出面积的表达式
,最后写出面积的表达式![]() ,再换元利用导数求它的最大值.
,再换元利用导数求它的最大值.
试题解析:
(1)由![]() ,令
,令![]() ,得
,得![]() ,所以
,所以![]() ,解得
,解得![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,故
,故![]() 所以在
所以在![]() 点的切线方程为
点的切线方程为![]() ,即
,即![]() ,同理可得在
,同理可得在![]() 点的切线方程为
点的切线方程为![]() .
.
(2)由题意得直线![]() 的斜率存在且不为0,
的斜率存在且不为0,
故设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 与
与![]() 联立,
联立,
得![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
故![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() 且
且![]() .
.
因为![]() 的中点为
的中点为![]() ,所以
,所以![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离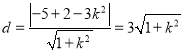 ,
,
所以![]()
![]() .
.
令![]() ,则
,则![]() ,则
,则![]() ,故
,故![]() .
.
设![]() ,则
,则![]() ,结合
,结合![]() ,令
,令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时, ![]() .
.


科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
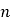
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,…,如图所示,在宝塔形数表中位于第![]() 行、第
行、第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]() ______.
______.
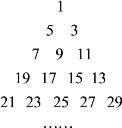
查看答案和解析>>
科目:高中数学 来源: 题型:
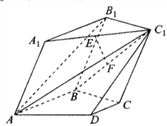
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为__________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线![]() 的参数方程为
的参数方程为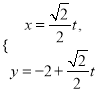 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为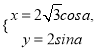 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和
和![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若![]() 为曲线
为曲线![]() 上的一个动点,求
上的一个动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有![]() 个粽子,其中豆沙粽
个粽子,其中豆沙粽![]() 个,肉粽
个,肉粽![]() 个,白粽
个,白粽![]() 个,这三种粽子的外观完全相同,从中任意选取
个,这三种粽子的外观完全相同,从中任意选取![]() 个.
个.
(![]() )求三种粽子各取到
)求三种粽子各取到![]() 个的概率.
个的概率.
(![]() )设
)设![]() 表示取到的豆沙粽个数,求
表示取到的豆沙粽个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com