
【题目】已知圆![]()
(1)求过点![]() 的圆的切线方程;
的圆的切线方程;
(2)点![]() 为圆上任意一点,求
为圆上任意一点,求![]() 的最值.
的最值.
【答案】(1) ![]() 和
和![]() (2)
(2)![]() 的最大值为
的最大值为![]() ;
;![]() 的最小值为
的最小值为![]()
【解析】
(1)本题首先可以确定圆的圆心以及半径,然后根据题意分为直线斜率存在以及不存在两种情况,最后根据圆心到切线距离等于半径即可列出算式并得出结果;
(2)本题首先可明确![]() 为原点到圆上一点的直线的斜率,然后结合图像得出当圆与直线相切时斜率取最值,最后根据圆心到切线距离等于半径即可得出结果.
为原点到圆上一点的直线的斜率,然后结合图像得出当圆与直线相切时斜率取最值,最后根据圆心到切线距离等于半径即可得出结果.
(1)因为圆的方程为![]() ,即
,即![]() ,
,
所以圆心为![]() ,半径为
,半径为![]() ,
,
①当切线斜率不存在时,
因为直线过点![]() ,所以直线方程为
,所以直线方程为![]() ,即
,即![]()
圆心到直线距离![]() ,所以直线
,所以直线![]() 是圆的切线,
是圆的切线,
②当切线斜率存在时,设切线斜率为![]() ,
,
则切线方程为![]() ,即
,即![]()
因为圆心到切线距离等于半径,
所以![]() ,解得
,解得![]() ,此时切线方程为
,此时切线方程为![]() ,
,
综上所述,过点![]() 的圆的切线方程为
的圆的切线方程为![]() 和
和![]() .
.
(2)因为![]() 即
即![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,
所以![]() 即原点到圆上一点的直线的斜率,
即原点到圆上一点的直线的斜率,
令![]() ,则原点到圆上一点的直线的方程为
,则原点到圆上一点的直线的方程为![]() ,即
,即![]()
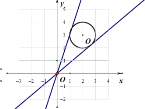
如图所示,当圆与直线相切时,斜率取最值,
则有圆心到切线距离等于半径,即![]() ,解得
,解得![]() 或
或![]() ,
,
所以斜率的最大值![]() ,斜率的最小
,斜率的最小![]() ,
,
所以![]() 的最大值为
的最大值为![]() ;
;![]() 的最小值为
的最小值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】(多选)下列命题中为真命题的是( )
A.若事件![]() 与事件
与事件![]() 互为对立事件,则事件
互为对立事件,则事件![]() 与事件
与事件![]() 为互斥事件
为互斥事件
B.若事件![]() 与事件
与事件![]() 为互斥事件,则事件
为互斥事件,则事件![]() 与事件
与事件![]() 互为对立事件
互为对立事件
C.若事件![]() 与事件
与事件![]() 互为对立事件,则事件
互为对立事件,则事件![]() 为必然事件
为必然事件
D.若事件![]() 为必然事件,则事件
为必然事件,则事件![]() 与事件
与事件![]() 为互斥事件
为互斥事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知以点
中,已知以点![]() 为圆心的
为圆心的![]() 及其上一点
及其上一点![]() .
.
(1)设圆![]() 与
与![]() 轴相切,与圆
轴相切,与圆![]() 外切,且圆心
外切,且圆心![]() 在直线
在直线![]() 上,求圆
上,求圆![]() 的标准方程;
的标准方程;
(2)设平行于![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级的一次月考成绩中随机抽取了 50名学生的成绩(满分100分,且抽取的学生成绩都在![]() 内),按成绩分为
内),按成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图.
五组,得到如图所示的频率分布直方图.
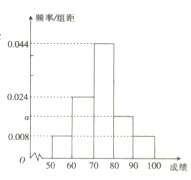
(1)用分层抽样的方法从月考成绩在![]() 内的学生中抽取6人,求分别抽取月考成绩在
内的学生中抽取6人,求分别抽取月考成绩在![]() 和
和![]() 内的学生多少人;
内的学生多少人;
(2)在(1)的前提下,从这6名学生中随机抽取2名学生进行调查,求月考成绩在![]() 内至少有1名学生被抽到的概率.
内至少有1名学生被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在意大利,有一座满是“斗笠”的灰白小镇阿尔贝罗贝洛(Alberobello),这些圆锥形屋顶的奇特小屋名叫Trullo,于1996年被收入世界文化遗产名录(如图1).现测量一个屋顶,得到圆锥SO的底面直径AB长为12m,母线SA长为18m(如图2).C,D是母线SA的两个三等分点(点D靠近点A),E是母线SB的中点.

(1)从点A到点C绕屋顶侧面一周安装灯光带,求灯光带的最小长度;
(2)现对屋顶进行加固,在底面直径AB上某一点P,向点D和点E分别引直线型钢管PD和PE.试确定点P的位置,使得钢管总长度最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 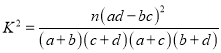 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com