
分析 由题意得a=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$,从而由对勾函数的性质可知f(x)=x+$\frac{1}{x}$在($\frac{1}{2}$,1)上是减函数,在[1,3)上是增函数,从而求实数a的取值范围.
解答 解:由题意得,x2-ax+1=0,
即a=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$,
由对勾函数的性质可知,
f(x)=x+$\frac{1}{x}$在($\frac{1}{2}$,1)上是减函数,在[1,3)上是增函数,
f($\frac{1}{2}$)=2+$\frac{1}{2}$=$\frac{5}{2}$,f(1)=1+1=2,f(3)=3+$\frac{1}{3}$=$\frac{10}{3}$;
故实数a的取值范围是$[{2,\frac{10}{3}})$.
故答案为:$[{2,\frac{10}{3}})$.
点评 本题考查了方程的根与函数的零点的关系应用及对勾函数的性质的应用.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:选择题
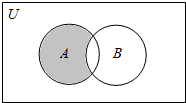
| A. | {x|x≥1} | B. | {x|0≤x≤1} | C. | {x|1≤x<2} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x}$ | B. | y=-tanx | C. | $y=\frac{{1-{2^x}}}{{1+{2^x}}}$ | D. | y=-x3(-1<x≤1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过500元部分 | 5% |
| 2 | 超过500元至2000元部分 | 10% |
| 3 | 超过2000元至5000元部分 | 15% |
| … | … | … |
| 9 | 超过100000元部分 | 45% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com