
分析 (1)若命题“若q,则p”为真,则q是p的充分条件,即可求实数a的取值范围;
(2)若p是¬q的充分条件,根据条件关系即可求实数a的取值范围.
解答 解:(1)由x2-4ax+3a2<0(a>0),得(x-a)(x-3a)<0,
则a<x<3a,
即p:x∈(a,3a),
若命题“若q,则p”为真,
即q是p的充分条件,即(2,3]⊆(a,3a),
即$\left\{\begin{array}{l}{a≤2}\\{3a>3}\end{array}\right.$,即$\left\{\begin{array}{l}{a≤2}\\{a>1}\end{array}\right.$,解得1<a≤2.
(2)¬q:x∈(-∞,2]∪(3,+∞),
若p是¬q的充分条件,
则(a,3a)⊆(-∞,2]∪(3,+∞),
∵a>0,
∴$\left\{\begin{array}{l}{a>0}\\{3a≤2}\end{array}\right.$或a≥3,
解得0<a≤$\frac{2}{3}$或a≥3,
即实数a的取值范围是0<a≤$\frac{2}{3}$或a≥3.
点评 本题主要考查复合命题与简单命题之间的关系,利用充分条件和必要条件的定义是解决本题的关键,


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{10}$) | B. | ($\frac{1}{10}$,1) | C. | (1,10) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
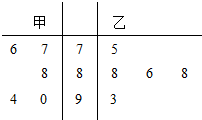 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com