
| A. | 16 | B. | 32 | C. | 31 | D. | 36 |
分析 根据题意,令x=$\frac{1}{2}$,求出a0,再令x=$\frac{3}{2}$,求出a0+a1+a2+…+an的值,即可求出n的值,再利用二项式展开式的通项公式求出展开式中x3的系数.
解答 解:∵(1+2x)n=a0+a1(x-$\frac{1}{2}$)+a2(x-$\frac{1}{2}$)2+…+an(x-$\frac{1}{2}$)n(其中n∈N*),
且a1+a2+…+an=240,
∴令x=$\frac{1}{2}$,得a0=${(1+2×\frac{1}{2})}^{n}$=2n;
再令x=$\frac{3}{2}$,得(1+2×$\frac{3}{2}$)n=a0+a1+a2+…+an=2n+240=4n,
解得2n=16,
∴n=4;
∴(1+2x)4展开式的通项公式为:
Tr+1=${C}_{4}^{r}$•(2x)r=${C}_{4}^{r}$•2r•xr,
令r=3,得出T4=${C}_{4}^{3}$•23•x3=32x3,
∴x3的系数32.
故选:B.
点评 本题考查了二项式定理的应用问题,也考查了用赋值法求对应项的系数问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{π}{4}$ | C. | -$\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AD}$=0 | C. | ABCD为矩形 | D. | ABCD为菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.
如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
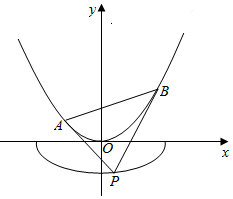 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com