Question

9．在三角形ABC中，点M是BC的中点，N在边AC上，且AN=2NC，AM与BN交与点P，则AP：PM=4：1．

Answer 1

分析 利用在三角形中，正弦定理之间的关系即可求解．

解答 解：由三角形ABC中，点M是BC的中点，N在边AC上，且AN=2NC，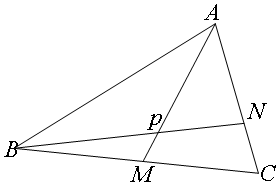
设BC=a，AN=2，NC=1，
在三角形APN中，由正弦定理可得：$\frac{AP}{sin∠ANP}=\frac{AN}{sin∠APN}$，即$\frac{AP}{sin∠ANP}=\frac{2}{sin∠APN}$…①，
在三角形BCN中，由正弦定理可得$\frac{BC}{sin∠BNC}=\frac{NC}{sin∠NBC}$，即$\frac{1}{sin∠NBC}=\frac{a}{sin∠BNC}$…②；
在三角形BMP中，由正弦定理可得$\frac{PM}{sin∠PBM}=\frac{\frac{BC}{2}}{sin∠BPM}$，即$\frac{PM}{sin∠PBM}=\frac{a}{2sin∠APN}$…③．
∵sin∠BNC=sin（π-∠PNA）=sin∠PNA
∴由①②③求解得：4PM=AP．
∴AP：PM=4：1．
故答案为：4：1

点评 本题考查了正弦定理的灵活运用和计算能力．属于中档题．