
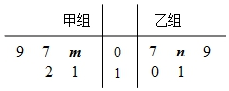
 ij���佫10������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ��������ͳ�����ݵľ�Ҷͼ��ͼ��ʾ����֪���鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9��
ij���佫10������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ��������ͳ�����ݵľ�Ҷͼ��ͼ��ʾ����֪���鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9������ ��1�������鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9�����þ�Ҷͼ�����m��n��
��2���ȷֱ����${{S}_{��}}^{2}$��${{S}_{��}}^{2}$�������鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9��${{S}_{��}}^{2}��{{S}_{��}}^{2}$���õ����鼼���ӹ�ˮƽ�ߣ�
��3���ʼಿ�ŴӸó���ס������鼼���и������ȡһ������������ӹ���������м�⣬�����˼ӹ��ĺϸ�������ֱ�Ϊ��a��b���������оٷ�������ó��䡰�����ϸĸ��ʣ�
��� �⣺��1�������鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9��
���ɾ�Ҷͼ�ã�$\left\{\begin{array}{l}{\frac{1}{5}��9+7+m+11+12��=9}\\{\frac{1}{5}��7+n+9+10+11��=9}\end{array}\right.$��
���m=6��n=8��
��2��${{S}_{��}}^{2}$=$\frac{1}{5}$[��6-9��2+��7-9��2+��9-9��2+��11-9��2+��12-9��2]=$\frac{26}{5}$��
${{S}_{��}}^{2}$=$\frac{1}{5}$[��7-9��2+��8-9��2+��9-9��2+��10-9��2+��11-9��2]=2��
�����鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9��${{S}_{��}}^{2}��{{S}_{��}}^{2}$��
�����鼼��ƽ������ȣ������鼼�����ȶ��������鼼���ӹ�ˮƽ�ߣ�
��3���ʼಿ�ŴӸó���ס������鼼���и������ȡһ������������ӹ���������м�⣬
�����˼ӹ��ĺϸ�������ֱ�Ϊ��a��b����
�����еģ�a��b���У�
��6��7������6��8������6��9������6��10������6��11������7��7������7��8������7��9������7��10����
��7��11������9��7������9��8������9��9������9��10������9��11������11��7������11��8������11��9����
��11��10������11��11������12��7������12��8������12��9������12��10������12��11��������25����
��a+b��17�Ļ����¼��У�
��6��7������6��8������6��9������6��10������6��11������7��7������7��8������7��9����
��7��10������9��7������9��8��������11����
������a+b��17�Ļ����¼�����14����
��ó��䡰�����ϸĻ����¼���14����
��ó��䡰�����ϸĸ���p=$\frac{14}{25}$��
���� ���⿼��ʵ��ֵ��������ʵ����ǻ����⣬����ʱҪ�������⣬ע�⾥Ҷͼ���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 19 | C�� | -1 | D�� | -10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com