考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,建立直角坐标系,则B(0,c),C(b,0),D(b,c),M(x,y).利用向量的坐标运算可得b
2+c
2=4.再利用数量积运算
•(
+
)=1,
可得bx+cy=1.利用数量积性质可得(x
2+y
2)(b
2+c
2)≥(bx+cy)
2,可得
||≥.再利用
+=1,
1=(bx+cy)(+)=
x2+y2++,可得x
2+y
2≤1,即可得出.
解答:
解:解:如图所示,建立直角坐标系.
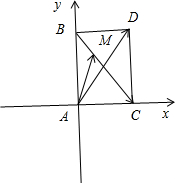
则B(0,c),C(b,0),D(b,c),M(x,y).
∵|
-
|=
||=2,
+=,及四边形ABDC为矩形,
∴
||=||=2.
∴b
2+c
2=4.
∵
•(
+
)=1,
∴bx+cy=1.
||=.
∵(x
2+y
2)(b
2+c
2)≥(bx+cy)
2,
∴4(x
2+y
2)≥1.
∴
≥.即
||≥.
∵点M在直线BC上,∴
+=1.
∴
1=(bx+cy)(+)=
x2+y2++,
∵b,c>0,x≥0,y≥0.
∴x
2+y
2≤1,即
≤1(当且仅当x=0或y=0时取等号),
综上可得:
≤||≤1.
故选:B.
点评:本题考查了向量的坐标运算、数量积运算及其性质、不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.




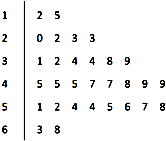 对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )
对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )