Question

11．如图，有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．设∠BAD=α
（Ⅰ）用α表示AD和CD的长；
（Ⅱ）写出梯形周长l关于角α的函数解析式，并求这个梯形周长的最大值．

Answer 1

分析 （I）过D、C分别作DE⊥AB、CF⊥AB，垂足分别为E、F，在Rt△ABD中，求出AD，在Rt△ADE中，求出AE，然后求解BC，CD即可．
（II）利用梯形ABCD的周长l=AB+BC+CD+AD，说明当点D接近于点A时，$α→\frac{π}{2}$，当点C、D接近重合时，$α→\frac{π}{4}$，得到l=-8cos²α+8cosα+8，（$\frac{π}{4}＜α＜\frac{π}{2}$），利用二次函数的性质，转化求解即可．

解答 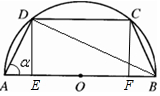（本题满分12分）
解：（I）过D、C分别作DE⊥AB、CF⊥AB，垂足分别为E、F，…（1分）
因为′AB为半圆的直径，AD⊥BD，又∠BAD=α
所以在Rt△ABD中，AD=AB•cosα=4cosα，…（3分）
又在Rt△ADE中，AE=AD•cosα=4cos²α，…（4分）
由等腰梯形ABCD同理可得，BC=4cosαBF=4cos²α，…（5分）
∴CD=EF=4-8cos²α；…（6分）
（II）∵梯形ABCD的周长l=AB+BC+CD+AD，
当点D接近于点A时，$α→\frac{π}{2}$，当点C、D接近重合时，$α→\frac{π}{4}$，
∴l=-8cos²α+8cosα+8，（$\frac{π}{4}＜α＜\frac{π}{2}$），…（8分）
$l=-8{（cosα-\frac{1}{2}）^2}+10$，…（10分）
∴当$cosα-\frac{1}{2}$，即$α=\frac{π}{3}$时，
梯形ABCD的周长l取最大值为10．…（12分）

点评 本题考查函数与方程的综合应用，三角函数的最值，考查转化思想以及计算能力．