
分析 (1)利用辅助角公式化简,再由($\frac{π}{6}$,1)与($\frac{2π}{3}$,-3)分别是函数图象上相邻的最高点和最低点列式求得c与ω的值,则函数解析式可求,再由复合函数的单调性求得函数的单调增区间;
(2)由$\overrightarrow{AB}•\overrightarrow{BC}$=-$\frac{1}{2}$ac求得角B,代入$f(B+\frac{π}{8})$,然后利用两角差的正弦求解.
解答 解:(1)∵f(x)=$\sqrt{3}$sinωx+cosωx+c=$2sin(ωx+\frac{π}{6})+c$.
且($\frac{π}{6}$,1)与($\frac{2π}{3}$,-3)分别是函数图象上相邻的最高点和最低点,
∴$\left\{\begin{array}{l}{\frac{T}{2}=\frac{2π}{3}-\frac{π}{6}}\\{ω=\frac{2π}{T}}\\{2sin(\frac{π}{6}•ω+\frac{π}{6})+c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{T=π}\\{c=-1}\\{ω=2}\end{array}\right.$.
∴$f(x)=2sin(2x+\frac{π}{6})-1$.
由$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$,k∈Z,解得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$,k∈Z.
∴函数f(x)的单调递增区间是[$kπ-\frac{π}{3},kπ+\frac{π}{6}$],k∈Z;
(2)∵在△ABC中,$\overrightarrow{AB}•\overrightarrow{BC}$=-$\frac{1}{2}$ac,
∴ac•cos(π-B)=-$\frac{1}{2}$ac,
∵0<B<π,∴B=$\frac{π}{3}$.
∴$f(B+\frac{π}{8})=2sin[(\frac{π}{3}+\frac{π}{8})+\frac{π}{6}]-1$
=$2sin\frac{13π}{12}-1=-2sin\frac{π}{12}-1$=$-2sin(\frac{π}{4}-\frac{π}{6})-1$
=$-2(sin\frac{π}{4}cos\frac{π}{6}-cos\frac{π}{4}sin\frac{π}{6})-1=\frac{\sqrt{2}-\sqrt{6}-2}{2}$.
点评 本题考查平面向量的数量积运算,考查三角形的解法,训练了三角函数中的恒等变换应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠BAD=α
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠BAD=α查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m?α,n?α,m∥β,n∥β,则α∥β | B. | m∥α,n∥β,且α∥β,则m∥n | ||
| C. | m⊥α,n?β,m⊥n,则α⊥β | D. | m⊥α,n⊥β,且α⊥β,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
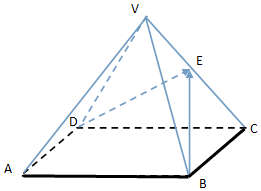 如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h
如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com