Question

【题目】已知函数 ．任取t∈R，若函数f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），记g（t）=M（t）﹣m（t）．
（1）求函数f（x）的最小正周期及对称轴方程；
（2）当t∈[﹣2，0]时，求函数g（t）的解析式；
（3）设函数h（x）=2|x﹣k|，H（x）=x|x﹣k|+2k﹣8，其中实数k为参数，且满足关于t的不等式 有解，若对任意x1∈[4，+∞），存在x2∈（﹣∞，4]，使得h（x2）=H（x1）成立，求实数k的取值范围．

Answer 1

【答案】
（1）解：函数 ，

则f（x）的最小正周期为 ；

令 ，解得f（x）的对称轴方程为x=2k+1（x∈Z）

（2）解：①当 时，在区间[t，t+1]上， ，

m（t）=f（﹣1）=﹣1，

∴ ；

②当 时，在区间[t，t+1]上， ，

m（t）=f（﹣1）=﹣1，

∴ ；

③当t∈[﹣1，0]时，在区间[t，t+1]上， ，

，

∴ ；

∴当t∈[﹣2，0]时，函数

（3）解：∵ 的最小正周期T=4，

∴M（t+4）=M（t），m（t+4）=m（t），

∴g（t+4）=M（t+4）﹣m（t+4）=M（t）﹣m（t）=g（t）；

∴g（t）是周期为4的函数，研究函数g（t）的性质，只须研究函数g（t）在t∈[﹣2，2]时的性质即可；

仿照（2），可得 ；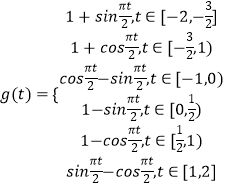

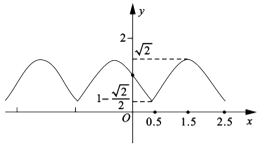
画出函数g（t）的部分图象，如图所示，

∴函数g（t）的值域为 ；

已知 有解，即 k≤4g（t）max=4 ，

∴k≤4；

若对任意x1∈[4，+∞），存在x2∈（﹣∞，4]，使得h（x2）=H（x1）成立，

即H（x）在[4，+∞）的值域是h（x）在（﹣∞，4]的值域的子集．

∵ ，

当k≤4时，∵h（x）在（﹣∞，k）上单调递减，在[k，4]上单调递增，

∴h（x）min=h（k）=1，

∵H（x）=x|x﹣k|+2k﹣8在[4，+∞）上单调递增，

∴H（x）min=H（4）=8﹣2k，

∴8﹣2k≥1，即 ；

综上，实数的取值范围是

【解析】（1）根据正弦型函数f（x）的解析式求出它的最小正周期和对称轴方程；（2）分类讨论 、 和t∈[﹣1，0]时，求出对应函数g（t）的解析式；（3）根据f（x）的最小正周期T，得出g（t）是周期函数，研究函数g（t）在一个周期内的性质，求出g（t）的解析式；画出g（t）的部分图象，求出值域，利用不等式 求出k的取值范围，再把“对任意x1∈[4，+∞），存在x2∈（﹣∞，4]，使得h（x2）=H（x1）成立”转化为“H（x）在[4，+∞）的值域是h（x）在（﹣∞，4]的值域的子集“，从而求出k的取值范围．