练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．（本题只限文科学生做）
    已知△ABC的两个顶点A（-10，2），B（6，4），垂心是H（5，2），求顶点C到直线AB的距离．

    分析 求出直线AC，BC的方程，可得C的坐标，求出直线AB的方程，利用点到直线的距离公式求出顶点C到直线AB的距离．

    解答 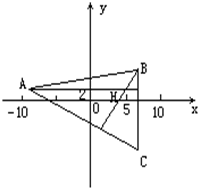解：∵${k_{BH}}=\frac{2-4}{5-6}=2$∴${k_{AC}}=-\frac{1}{2}$
    ∴直线AC的方程为$y-2=-\frac{1}{2}（x+10）$即x+2y+6=0   （1）
    又∵kAH=0，
    ∴BC所直线与x轴垂直  
    故直线BC的方程为x=6   （2）
    解（1）（2）得点C的坐标为C（6，-6）…（8分）
    由已知直线AB的方程为：x-8y+26=0，
    ∴点C到直线AB的距离为：
    d=$\frac{{|{6-8×（-6）+26}|}}{{\sqrt{1+64}}}$=$\frac{{16\sqrt{65}}}{13}$…（12分）

    点评 本题考查直线方程，考查点到直线的距离公式，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．过两点（-1，0），（0，1）的直线方程为：（　　）
    A．x-y+1=0B．x-y-3=0C．2x-y=0D．2x-y-3=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某同学参加4门学科的学业水平考试，假设该同学第一门学科取得优秀成绩的概率为$\frac{2}{3}$，第二门学科取得优秀成绩的概率为$\frac{4}{5}$，第三、第四门学科取得优秀成绩的概率分别为m，n（m＞n），且不同学科是否取得优秀成绩相互独立，记ξ为该同学取得优秀成绩的课程数，其分布列为如下表：
    ξ01234
    p$\frac{1}{120}$xyz$\frac{1}{5}$
    （1）求该生至少有1门课程取得优秀成绩的概率；
    （2）求m，n的值；
    （3）求数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．有2人从一座6层大楼的底层进入电梯，假设每个人自第二层开始在每一层离开电梯是等可能的，则该2人在不同层离开电梯的概率是（　　）
    A．$\frac{1}{6}$B．$\frac{1}{5}$C．$\frac{4}{5}$D．$\frac{5}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．直线（cos$\frac{π}{6}$）x+（sin$\frac{π}{6}$）y+2=0的倾斜角为（　　）
    A．$\frac{π}{6}$B．$\frac{5π}{6}$C．$\frac{π}{3}$D．$\frac{2π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数$f（x）=\left\{\begin{array}{l}lo{g_2}x+2，x＞0\\{3^x}，x≤0\end{array}\right.$，则$f[f（\frac{1}{8}）]$的值（　　）
    A．3B．$\frac{1}{3}$C．-3D．$-\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若点$M（a，\frac{1}{b}）$和$N（b，\frac{1}{c}）$都在直线l：x+y=1上，又点P$（c，\frac{1}{a}）$和点$Q（\frac{1}{c}，b）$，则（　　）
    A．点P和Q都不在直线l上B．点P和Q都在直线l上
    C．点P在直线l上且Q不在直线l上D．点P不在直线l上且Q在直线l上

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知向量$\vec m$与$\vec n$的夹角是$\frac{π}{3}$，且$（{\vec m-\vec n}）•\vec m=0$，则$\frac{{|{\vec m}|}}{{|{\vec n}|}}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1（-c，0），F2（c，0），M为椭圆上的一点，且满足∠F1MF2=$\frac{π}{3}$．
    （1）求椭圆离心率的取值范围；
    （2）当椭圆的离心率e取得最小值时，点N$（0，3\sqrt{3}）$到椭圆上的点的最远距离为4$\sqrt{3}$，求此时椭圆C的方程．

    查看答案和解析>>

    同步练习册答案