
分析 (1)由a1=1,Sn+1=3Sn+2(n>1,n∈N*),得Sn=3Sn-1+2(n>1,n∈N*),两式相减得:an+1=3an,由此能求通项公式,
(2)化简bn=n•($\frac{1}{3}$)n-1,n≥2,利用错位相减法即可求出数列{bn}的前n项和Tn.,
解答 解:(1)∵a1=1,Sn+1=3Sn+2(n>1,n∈N*),①
∴Sn=3Sn-1+2(n>1,n∈N*),②
②-①,得:an+1=3an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=3,
当n=2时,S2=a2+a1=3a1+2,
∴a2=4,
∴{an}是首项为2,公比为3的等比数列,n≥2
∴an=4×3n-2,
当n=1时,a1=1
∴an=$\left\{\begin{array}{l}{1,n=1}\\{4•{3}^{n-2},n≥2}\end{array}\right.$;
(2)当n=1时,b1=$\frac{8}{{a}_{2}-{a}_{1}}$=$\frac{8}{3}$,T1=b1=$\frac{8}{3}$,
当n≥2时,bn=$\frac{8n}{{a}_{n+1}-{a}_{n}}$=$\frac{8n}{4•{3}^{n-1}-4•{3}^{n-2}}$=n•($\frac{1}{3}$)n-2,
当n≥2时,Tn=$\frac{8}{3}$+2×($\frac{1}{3}$)0+3×($\frac{1}{3}$)1+4×($\frac{1}{3}$)2+…+n•($\frac{1}{3}$)n-2,
∴$\frac{1}{3}$Tn=$\frac{8}{9}$+2×($\frac{1}{3}$)1+3×($\frac{1}{3}$)2+…+(n-1)×($\frac{1}{3}$)n-2+n•($\frac{1}{3}$)n-1,
∴$\frac{2}{3}$Tn=$\frac{25}{9}$+($\frac{1}{3}$)0+($\frac{1}{3}$)1+($\frac{1}{3}$)2+($\frac{1}{3}$)3+…+($\frac{1}{3}$)n-2-n•($\frac{1}{3}$)n-1
=$\frac{25}{9}$+$\frac{1-\frac{1}{{3}^{n-1}}}{1-\frac{1}{3}}$-n•($\frac{1}{3}$)n-1=$\frac{77}{18}$-($\frac{3}{2}$+n)($\frac{1}{3}$)n-1,
∴Tn=$\frac{77}{12}$-($\frac{n}{2}$+$\frac{3}{4}$)•($\frac{1}{3}$)n-2.
点评 本题考查数列的通项公式的求法,是中档题,解题时要注意构造法的合理运用.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
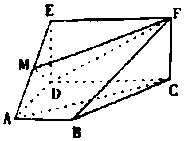 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{lnx}{x}$)′=$\frac{lnx-1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (2x)′=2x$\frac{1}{ln2}$ | D. | (xsinx)′=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,求角C的值..
(1)设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,求角C的值..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com