
| A. | 1 | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 本题是向量的坐标表示的应用,结合图形,利用三角函数的性质,即可求出结果.
解答 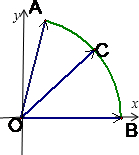 解:∵两个单位向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为60°,点C在以O圆心的
解:∵两个单位向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为60°,点C在以O圆心的
圆弧AB上移动,$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,
建立如图所示的坐标系,则B(1,0),A(cos60°,sin60°),
即A($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
设∠BOC=α,则$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$=(cosα,sinα)=($\frac{1}{2}$x+y,$\frac{\sqrt{3}}{2}$x),
∴$\left\{\begin{array}{l}{cosα=\frac{x}{2}+y}\\{sinα=\frac{\sqrt{3}}{2}x}\end{array}\right.$∴x=$\frac{2}{\sqrt{3}}$sinα,y=cosα-$\frac{1}{\sqrt{3}}$sinα,
∴x+y=cosα+$\frac{1}{\sqrt{3}}$sinα=$\frac{2\sqrt{3}}{3}$sin(α+60°).
∵0°≤α≤60°,∴60°≤α+60°≤120°,∴$\frac{\sqrt{3}}{2}$≤sin(α+60°)≤1,
故当α+60°=90°时,x+y取得最大值为$\frac{2\sqrt{3}}{3}$,
故选:D.
点评 本题考查向量知识的运用,考查三角函数的性质,确定x,y的关系式是关键,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{2}$ | B. | -1 | C. | -1或$\sqrt{2}$ | D. | -1或$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
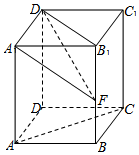 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为$\sqrt{2}$的正方形,AA1=3,点F在棱B1B上运动.
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为$\sqrt{2}$的正方形,AA1=3,点F在棱B1B上运动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | ab>1 | D. | lg(b-a)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | D. | $y=\sqrt{x}+\frac{4}{{\sqrt{x}}}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M | B. | N | C. | M∩∁UN | D. | N∩∁UM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com