
分析 (1)通过${C}_{2n}^{r}$=${C}_{2n}^{2n-r}$,利用倒序相加法计算即得结论;
(2)利用(1+x)2n=(1+x)n•(1+x)n,并两端分别展开,通过等式两端xn的系数相等及${C}_{2n}^{r}$=${C}_{2n}^{2n-r}$,化简即得结论;
(3)利用二项式定理将f(x)=(1+x)2n、g(x)=(1-x)2n并展开相加,然后利用|x|<1放缩,通过逆用二项式定理即得结论.
解答 证明:(1)记C2n1+2C2n2+3C2n3+…+2nC2n2n=t,
则由${C}_{2n}^{r}$=${C}_{2n}^{2n-r}$可知,C2n2n-1+2C2n2n-2+3C2n2n-3+…+2nC2n0=t,
两式相加得:2t=2n[C2n0+C2n1+C2n2+C2n3+…+C2n2n],
又∵f(1)=(1+1)2n=C2n0+C2n1+C2n2+C2n3+…+C2n2n,
∴t=n•22n,即C2n1+2C2n2+3C2n3+…+2nC2n2n=n22n;
(2)∵f(x)=(1+x)2n=(1+x)n•(1+x)n,
∴C2n0+C2n1x+C2n2x2+C2n3x3+…+C2n2nx2n=(Cn0+Cn1x+Cn2x2+Cn3x3+…+Cnnxn)•(Cn0+Cn1x+Cn2x2+Cn3x3+…+Cnnxn),
比较等式两端xn的系数可知,${C}_{n}^{0}$${C}_{n}^{n}$+${C}_{n}^{1}$${C}_{n}^{n-1}$+…+${C}_{n}^{n}$${C}_{n}^{0}$=${C}_{2n}^{n}$,
又∵${C}_{2n}^{r}$=${C}_{2n}^{2n-r}$,
∴(Cn0)2+(Cn1)2+(Cn2)2+…+(Cnn)2=C2nn;
(3)∵f(x)=(1+x)2n,g(x)=(1-x)2n,
∴f(x)=C2n0+C2n1x+C2n2x2+C2n3x3+…+C2n2nx2n,
g(x)=C2n0-C2n1x+C2n2x2-C2n3x3+…+(-1)r${C}_{2n}^{2n-r}$xr+…+C2n2nx2n,
∵|x|<1,n∈N+,
∴xr<1(r=0,1,2,…,2n),
∴f(x)+g(x)=[C2n0+C2n1x+C2n2x2+C2n3x3+…+C2n2nx2n]+[C2n0-C2n1x+C2n2x2-C2n3x3+…+(-1)r${C}_{2n}^{2n-r}$xr+…+C2n2nx2n]
=2[C2n0+C2n2x2+…+${C}_{2n}^{2n-2r}$x2r+…+C2n2nx2n]
<2[C2n0+C2n2+…+${C}_{2n}^{2n-2r}$+…+C2n2n]
=[C2n0+C2n1+C2n2+C2n3+…+C2n2n]+[C2n0-C2n1+C2n2-C2n3+…+(-1)r${C}_{2n}^{2n-r}$+…+C2n2n]
=(1+1)2n+(1-1)2n
=4n.
点评 本题考查二项式定理的应用,考查运算求解能力,注意解题方法的积累,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
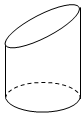 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 135° | C. | 120° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com