
分析 (1)当P为椭圆的上下顶点时,△PF1F2面积的最大值,利用面积公式、离心率公式及a2=b2+c2,联立解出即可得出a、b和c的值,求得椭圆方程,由$\frac{p}{2}$=c,求得p的值,即可求得抛物线方程;
(2)设出直线方程和A、B点坐标,并将直线方程代入椭圆方程,整理得到关于y的一元二次方程,利用韦达定理求得y1+y2和y1•y1关系,$\overrightarrow{OA}$•$\overrightarrow{OB}$=5,求得t=5,即可证明直线AB必过定点(5,0),设G、H的坐标,分别表示出丨AB丨和丨GH丨,根据四边形AGBH面积S=$\frac{1}{2}$丨AB丨•丨GH丨,整理关于x的函数,利用函数单调性求得S的最小值.
解答 解:(1)设F1(-c,0),F2(c,0),由题意得:
$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{\frac{1}{2}(2c)×b=\sqrt{3}}\end{array}\right.$,解得:a=2,b=$\sqrt{3}$,c=1,
所以椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.(2分)
所以$\frac{p}{2}=1$,得:p=2.
抛物线E的方程为y2=4x.(3分)
(2)①证明:设直线AB的方程为x=my+t,A($\frac{{y}_{1}^{2}}{4}$,y1),B($\frac{{y}_{2}^{2}}{4}$,y2),y1•y1<0,
联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+t}\end{array}\right.$得:y2-4my-4t=0,
由韦达定理可知y1+y2=4m,y1•y1=-4t.(5分)
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=5.,得$\frac{({y}_{1}{y}_{2})^{2}}{16}+{y}_{1}{y}_{2}=-5$,
整理得t2-4t-5=0,解得t=-1或5,
∵y1•y1<0,
∴t=5,
∴直线AB过定点M的坐标为(5,0).(7分)
②由①得丨AB丨=$\sqrt{1+{m}^{2}}$,丨y1-y1丨=$\sqrt{1+{m}^{2}}$•$\sqrt{16{m}^{2}+80}$=4$\sqrt{1+{m}^{2}}$•$\sqrt{{m}^{2}+5}$.(9分)
设G(x3,y3)、H(x4,y4),同理得:丨GH丨=$\sqrt{1+(-\frac{1}{m})^{2}}$丨y3-y4丨=4$\sqrt{1+\frac{1}{{m}^{2}}}$•$\sqrt{\frac{1}{{m}^{2}}+5}$.(10分)
则四边形AGBH的面积S=$\frac{1}{2}$丨AB丨•丨GH丨=8$\sqrt{1+{m}^{2}}$•$\sqrt{{m}^{2}+5}$•$\sqrt{1+\frac{1}{{m}^{2}}}$•$\sqrt{\frac{1}{{m}^{2}}+5}$.
=8$\sqrt{[2+({m}^{2}+\frac{1}{{m}^{2}})]•[26+5({m}^{2}+\frac{1}{{m}^{2}})]}$,(11分)
令${m}^{2}+\frac{1}{{m}^{2}}$=μ(μ≥2),
则S=8$\sqrt{(2+μ)(26+5μ)}$=8$\sqrt{5{μ}^{2}+36μ+52}$,
∴S关于μ的增函数.故Smin=96,当且仅当m=±1时取得最小值96.(12分)
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、四边形形面积计算公式、向量数量积运算性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则cos2θ-sinθ2+2=( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则cos2θ-sinθ2+2=( )| A. | $\frac{57}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{57}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,a>b是sinA>sinB的充要条件 | |
| B. | 命题:“在锐角△ABC中,sinA>cosB”为真命题 | |
| C. | 若p:?x≥0,x2-x+1>0,则¬p:?x<0,x2-x+1≤0 | |
| D. | 已知命题p:?φ∈R,使f(x)=sin(x+φ)为偶函数;命题q:?x∈R,cos2x+4sinx-3<0,则“p∧(¬q)”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$-1,$\sqrt{5}$-1) | B. | [-$\sqrt{5}$-1,$\sqrt{5}$-1] | C. | (-2$\sqrt{2}$-1,2$\sqrt{2}$-1) | D. | [-2$\sqrt{2}$-1,2$\sqrt{2}$-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$) | C. | (0,$\frac{π}{6}$) | D. | (0,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
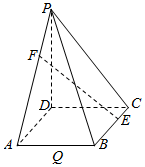 如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | ±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com