
| A. | 在△ABC中,a>b是sinA>sinB的充要条件 | |
| B. | 命题:“在锐角△ABC中,sinA>cosB”为真命题 | |
| C. | 若p:?x≥0,x2-x+1>0,则¬p:?x<0,x2-x+1≤0 | |
| D. | 已知命题p:?φ∈R,使f(x)=sin(x+φ)为偶函数;命题q:?x∈R,cos2x+4sinx-3<0,则“p∧(¬q)”为真命题 |
分析 A.根据正弦定理进行判断.
B.根据三角函数的诱导公式进行化简
C.根据特称命题的否定是全称命题进行判断
D.根据复合命题真假关系进行判断.
解答 解:A.在△ABC中,由正弦定理得a>b是sinA>sinB的充要条件,故A正确,
B.在在锐角△ABC中,A+B>$\frac{π}{2}$,则A>$\frac{π}{2}$-B,
则sinA>sin($\frac{π}{2}$-B)=cosB,即sinA>cosB成立,故B正确,
C.若p:?x≥0,x2-x+1>0,则¬p:?x≥0,x2-x+1≤0,故C错误,
D.当φ=$\frac{π}{2}$时,f(x)=sin(x+φ)=cosx为偶函数,则命题p是真命题,
cos2x+4sinx-3=1-2sin2x+4sinx-3=-2(sinx-1)2≤0,
即:?x∈R,cos2x+4sinx-3≤0,故命题q是假命题,则“p∧(¬q)”为真命题,故D正确,
故选:C
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,但一般难度不大.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{4}{3}$x | B. | y=±$\frac{\sqrt{3}}{2}$x | C. | y=±$\frac{9}{16}$x | D. | y=±$\frac{3}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 共线向量的夹角为0°或180° | |
| B. | 长度相等的向量叫做相等向量 | |
| C. | 共线向量就是向量所在的直线在同一直线上 | |
| D. | 零向量没有方向 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40m,并在点C测得塔顶A的仰角为30°.则塔高AB为( )m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40m,并在点C测得塔顶A的仰角为30°.则塔高AB为( )m.| A. | 20 | B. | 20$\sqrt{2}$ | C. | 20$\sqrt{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
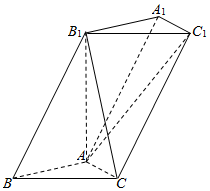 如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,B1C=2,∠ABB1=60°.
如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,B1C=2,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com