Question

6．已知正四棱锥P-ABCD的各顶点在同一个球O的球面上，且该棱锥的体积为$\frac{{3\sqrt{2}}}{2}$，底面边长为$\sqrt{3}$，则球O的表面积为8π．

Answer 1

分析 正四棱锥P-ABCD的五个顶点在同一球面上，则其外接球的球心在它的高PO₁上，记为O，如图．求出AO₁，OO₁，解出球的半径，求出球的表面积．

解答 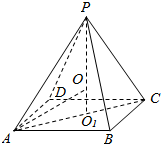解：∵棱锥的体积为$\frac{{3\sqrt{2}}}{2}$，底面边长为$\sqrt{3}$，
∴高h=$\frac{{3\sqrt{2}}}{2}$，
正四棱锥P-ABCD的外接球的球心在它的高PO₁上，
记为O，PO=AO=R，PO₁=$\frac{{3\sqrt{2}}}{2}$，OO₁=$\frac{{3\sqrt{2}}}{2}$-R，
在Rt△AO₁O中，AO₁=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{3}}{2}$，由勾股定理R²=3+（$\frac{{3\sqrt{2}}}{2}$-R）²得R=$\sqrt{2}$，
∴球的表面积S=8π
故答案为：8π．

点评 本题考查球的表面积，球的内接体问题，解答关键是确定出球心的位置，利用直角三角形列方程式求解球的半径．需具有良好空间形象能力、计算能力．