考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)以{
,,}为单位正交基底建立空间直角坐标系A-xyz,利用向量法能求出异面直线A
1B与C
1D所成角的余弦值.
(2)分别求出平面ABA
1的法向量和平面ADC
1的法向量,利用向量法能求出平面ADC
1与ABA
1所成二面角的余弦值,再由三角函数知识能求出平面ADC
1与ABA
1所成二面角的正弦值.
解答:
解:(1)以{
,,}为单位正交基底建立空间直角坐标系A-xyz,
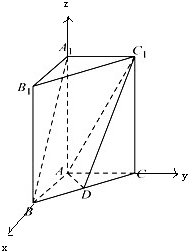
则由题意知A(0,0,0),B(2,0,0),C(0,2,0),
A
1(0,0,4),D(1,1,0),C
1(0,2,4),
∴
=(2,0,-4),
=(1,-1,-4),
∴cos<
,>=
=
=
,
∴异面直线A
1B与C
1D所成角的余弦值为
.
(2)
=(0,2,0) 是平面ABA
1的一个法向量,
设平面ADC
1的法向量为
=(x,y,z),
∵
=(1,1,0),=(0,2,4),
∴
,取z=1,得y=-2,x=2,
∴平面ADC
1的法向量为
=(2,-2,1),
设平面ADC
1与ABA
1所成二面角为θ,
∴cosθ=|cos<
,>|=|
|=
,
∴sinθ=
=
.
∴平面ADC
1与ABA
1所成二面角的正弦值为
.
点评:本题考查两条异面直线所成角的余弦值的求法,考查平面与平面所成角的正弦值的求法,解题时要注意向量法的合理运用.

 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.


 阅读快车系列答案
阅读快车系列答案 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.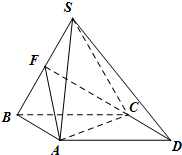 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.